VM-LSDYNA-FLUID-007
VM-LSDYNA-FLUID-007
Unsteady 3D Laminar Flow Around Cylinder in a Channel
Overview
| Reference: |
Schäfer, M., Turek, S., Durst, F., Krause, E., & Rannacher, R. (1996). Benchmark computations of laminar flow around a cylinder. In: Hirschel, E.H. (eds) Flow simulation with high-performance computers II. Notes on numerical fluid mechanics (NNFM), vol 48. Vieweg+Teubner Verlag (pp.547–566). Balmus, M., Hoffman, J., Massing, A., & Nordsletten, D.A. (2022). A stabilized multidomain partition of unity approach to solving incompressible viscous flow. Computer Methods in Applied Mechanics and Engineering, 392 (2), p.114656. |
| Analysis Type(s): | Incompressible CFD |
| Input Files: | Link to Input Files Download Page |
Test Case
This test case reproduces a three-dimensional, unsteady, incompressible laminar flow around a cylinder inside a channel. The purpose of the test case is to validate the maximum drag and lift force coefficients and the pressure difference between the front and rear points of the cylinder.
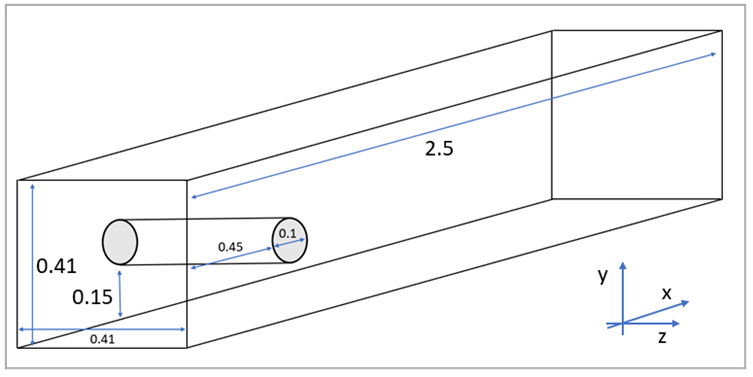
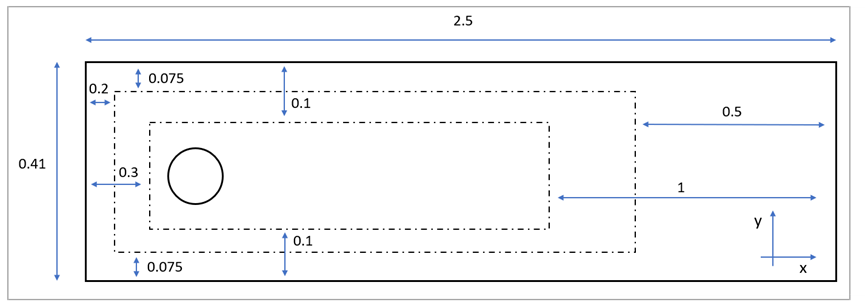
The domain consists of a box (the channel) with an inflow at prescribed velocity, an outflow at prescribed pressure, and the lateral sides of the boundary with non-slip conditions (the channel walls). The cylinder also features a non-slip condition. The domain size and relevant quantities are shown in Figure 157. As you can see, the cylinder location is not perfectly symmetrical with respect to the channel height in the y direction. Two meshing boxes have been used to selectively refine the mesh around the cylinder and its wake (see Figure 158). For this test case, all units of measure are consistent (length = m, time = s, mass = kg, force = N, pressure = Pa).
| Material Properties | Geometric Properties | Loading |
|---|---|---|
|
Fluid: Fluid density ρ = 1 Inflow max velocity in channel’s axial direction Um = 2.25 Flow dynamic viscosity μ = 10-3 |
Mesh size: Fluid boundaries elements size: 0.01 Cylinder elements size: 0.001 Anisotropic elements added to cylinder Boundary Layer: 6 Anisotropic elements added to channel boundary layer: 4 Geometry: Cylinder diameter D = 0.1 Channel height/width H = 0.41 |
Fluid: Outflow pressure p = 0 |
Analysis Assumptions and Modeling Notes
The behavior of the flow is characterized by the Reynolds number
(24) |
where is the fluid's density,
is the characteristic length of the problem (the cylinder diameter), and
is the dynamic viscosity of the flow.
is the flow mean velocity at the channel's inlet
(25) |
where is the (unsteady) velocity field in the channel's axial direction, which is
imposed at the inlet (x = 0). The complete inflow velocity
field relation is
(26) |
where is the maximum inflow velocity in the channel's axial direction. This yields
a Reynolds number
.
In this study, the time interval is
0 ≤t ≤ 8. The values of drag
and lift coefficients (respectively, and
) are plotted, and their maximum value (
and
) will be compared to the same values available in the reference. The
nondimensional coefficients are evaluated using the following relationship:
(27) |
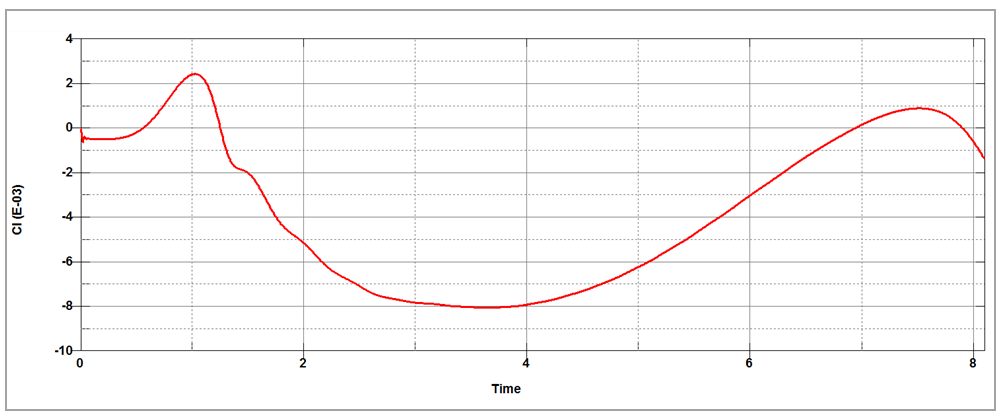
where 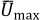 is the maximum of
is the maximum of for the considered time interval and
is the relative dimensional force on the cylinder surface. The drag force is
the resultant force on the cylinder in the asymptotic flow direction (x direction), the lift
force is the resultant force on the cylinder orthogonal to the asymptotic flow direction (y
direction), and both forces are the sum of pressure and viscous forces.
As a further reference value, the pressure difference is defined, with the front and end points of the cylinder
(xa, ya,
za) = (0.45, 0.2, 0.205) and
(xb,yb,
zb) = (0.55, 0.2, 0.205),
respectively. The value
will be compared to the same value in the reference.
A picture of the domain's mesh is shown in Figure 159, while Figure 160 shows a detail of the mesh refinement around the cylinder and the channel's walls.
Results Comparison
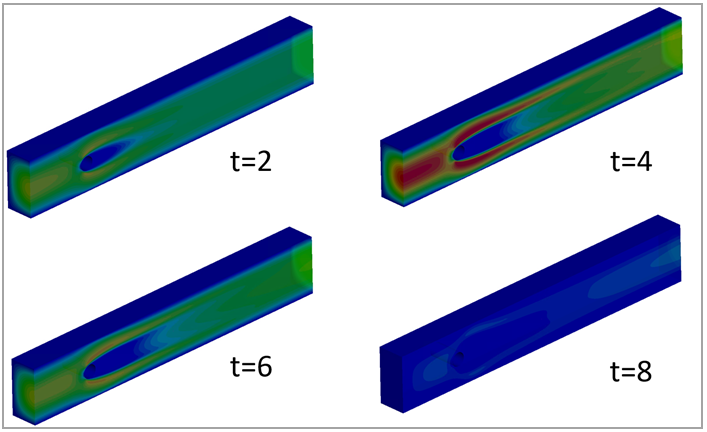
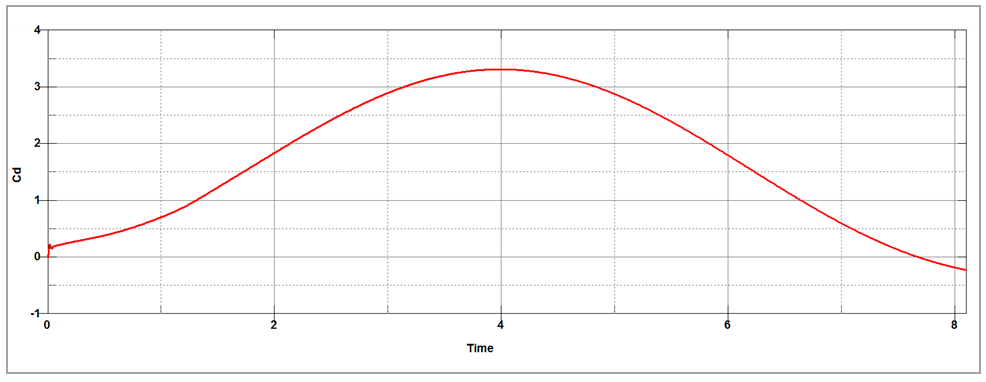
Figure 161 shows the flow velocity contours on the channels' outer surfaces and on a transparent section in the x-y plane for z = 0.205 at different times. You can see the symmetric, laminar, unsteady separation downstream of the cylinder, as well as the boundary layer development along the channel walls. Figure 162 and Figure 163 show respectively the drag and the lift coefficients of the cylinder over time for the current analysis.
The results table below shows a comparison of the maximum drag and lift coefficients
( and
) and the pressure difference
between the present analysis and the reference. The reference proposes a
comparison of the same values calculated with a variety of different numerical methods. The
value below shown in the target column is the average between the upper and lower bounds for
each variable. In the case of
, the error with respect to the benchmark is higher. This is common in the
literature. The main reason is that
is sensibly higher than
, meaning that the refinement errors are more likely to impact accuracy (see
reference Balmus et al. (2022)).
| Results | Target | LS-DYNA | Error (%) |
|---|---|---|---|
| 3.2500 | 3.3219 | 2.21% | |
| 0.0030 | 0.0080 | 168.3% | |
| –0.1000 | -0.1089 | 8.99% |