Computing and
, defined in Equation 17–39, involves evaluations of spatial gradients for various quantities
at face centers. Applying Green-Gauss theorem the gradient of a scalar
at face center
is computed as,
(17–48) |
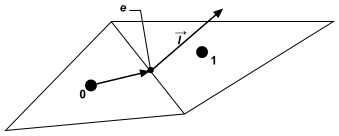
where the subscript represents the center of each edge of a film face,
the area of the face and
the length vector (whose magnitude is the
length of the edge and whose direction is normal to the edge), as
in the sketch below,
Clearly, at the center of the gradient calculation is how to
obtain . The following describes the steps taken
in the current implementation.
(1) Primary gradient computation
A primary gradient is calculated using Green-Gauss theorem by simply estimating edge center value as,
(17–49) |
(17–50) |
(2) Reconstruction of edge-center values
The edge-center values are then computed using either the first-order upwind or the second-order upwind schemes,
1st-order upwind:
2nd-order upwind:
is the value
of
at the UPWIND face center;
is the distance vector from the UPWIND face center
to the edge center.
(3) Final gradient calculation
Finally the gradient at face center is computed as,
(17–51) |