The majority of industrially important disperse multiphase-flows are confined flows, such as flows in cyclone separators or in pneumatic conveying pipe systems. The motion of large particles, which is dominated by inertia, is strongly influenced by the confinement. Studies of the wall-collision process have shown that irregularities due to wall-roughness and deviation of particle shape from a sphere play important roles [208], [209], [210].
To account for the influence of wall roughness on the particle-wall collision, the irregular bouncing model of Frank [211] is used. This model is based on the virtual wall model that was proposed by Sommerfeld [212].
Figure 6.11: Particle-Wall Interaction at a rough wall. Definition of Δγ and characteristic roughness element length scales
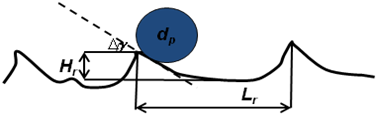
In this model, it is assumed that the reflection of a particle
at a rough wall can be modeled as the reflection of the particle at
a virtual wall that is inclined with an angle of relative to the real wall. The inclination angle
is a function of the wall roughness scale and the
particle diameter.
In the model of Frank [4] the inclination angle, , is sampled from a Gaussian distribution with a
mean value of 0° and a standard deviation of
. The standard deviation depends
on the particle diameter
and the roughness parameters.
It is estimated as:
(6–185) |
where:
is the mean cycle of roughness (the average distance between peaks of wall material)
is the mean roughness height
is the standard deviation of the roughness height


