Often a physical problem has the property that all aspects of the flow are symmetric about some physical (flat) plane. A problem is symmetric about a plane when the flow on one side of the plane is a mirror image of flow on the opposite side. By definition, a symmetry boundary condition refers to a planar boundary surface.
A particular case may have more than one plane of symmetry. For example, the flow in a square duct may exhibit symmetry about two independent planes (at 90° to one another). In this case, the physical problem has four-way symmetry. The computational domain can therefore be limited to one quarter of the duct, using two Symmetry Plane boundaries.
If you have two surfaces that meet at a sharp angle, and both are symmetry planes, you should set each surface to be a separate named boundary condition, rather than combine them into a single one.
When using an SMC turbulence model, you should position your model so that symmetry planes are perpendicular to coordinate axes if possible. This improves the performance of the CFX-Solver.
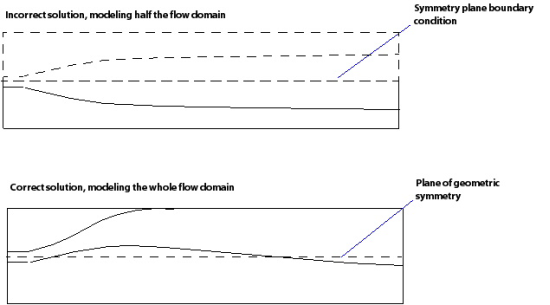
Symmetric geometry does not necessarily imply that the flow field is also symmetric. For example, a jet entering at the center of a symmetrical duct will tend to flow along one side above a certain Reynolds number. This is known as the Coanda effect. If a symmetry plane is used in this situation, an incorrect flow field will be obtained.
A symmetry plane should only be used when you have reason to believe that the flow field is also symmetrical.
A description of the mathematical details of the Symmetry Plane boundary condition is available in Symmetry Plane in the CFX-Solver Theory Guide.