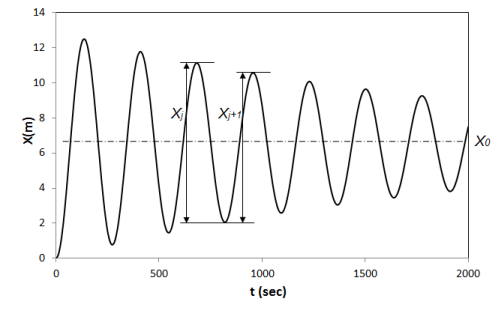
The damping property for a specified degree of freedom of a
floating structure can be estimated using a numerical twang test record.
As shown in Figure 14.4: Freely-Decaying Record, the structure center
of gravity is shifted by a distance along the specified degree of freedom from its equilibrium position
in still water at time
. A time history of its freely-decaying response
can then be calculated by an Aqwa time domain analysis.
Assuming that the motion in this degree of freedom has no interaction with other motions, and that there are no other external dynamic forces, the linear single degree of freedom dynamic system has an analytical response of the form:
(14–16) |
where ωn
is the natural frequency, is the damped
natural frequency, and
is the required percentage of critical damping denoted
in Equation 11–22.
The percentage of critical damping may be measured by the logarithmic decrement [7]
(14–17) |
where and
are the heights of two successive maxima.
Based on the linear dynamic system assumption, the ratio of
the heights of two successive maxima is approximately equal to the
square of the ratio of the heights of a crest-trough and its adjacent
trough-crest, such as and
shown in Figure 14.4: Freely-Decaying Record. The linear percentage of critical damping
can therefore be estimated by
(14–18) |
where .
From Equation 14–18, it should be noted that the calculated percentage of critical damping may vary over time. To further investigate this time-dependent variation, a nonlinear representation of the damping property can be introduced as
(14–19) |
where is the equivalent velocity amplitude within one natural period, and the
quadratic and linear terms are given by
(14–20) |
Using the definition in Equation 11–22, the ratio of the nonlinear damping and mass can be derived from Equation 14–19,
(14–21) |
where .