The convolution integration approach discussed in Radiation Force by Convolution Integration can be used in the time domain analysis for estimating the sloshing force of the internal tank.
The added mass matrix is selected to calculate the impulse function defined by Equation 13–4,
(13–9) |
where is the added mass matrix of the internal tank with respect to the LSA origin
motions in the FRA which is define by Equation 4–107, Σ indicates the
summation of the added mass matrices of the internal tanks attached on that structure.
is the added mass matrix at infinite frequency, which should have been
calculated in the frequency domain analysis.
The equation of motion expressed in Equation 13–3 is still valid for the structures with internal tanks. Note that the assembled matrices of A ∞, K and h, which consist of the contributions of both the external water and the internal tank liquids, must be employed in this equation.
If the RAO-based radiation and sloshing forces are required for motion response calculation at each time, the assembled added and damping matrices including the internal tank effects should be used in Equation 13–8.
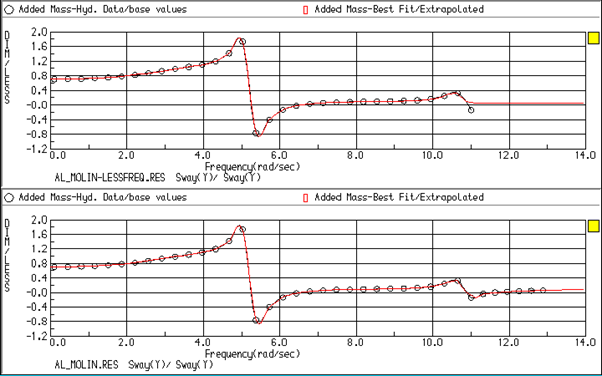
Note: The maximum frequency in the hydrodynamic database should not be close to any of the internal tank’s sloshing resonant frequencies in order to give a better quality of the added mass extrapolation to calculate the impulse function in Equation 13–9. As shown in Figure 13.1: Added Mass and its Extrapolation for Impulse Function Estimation, the maximum frequency of the hydrodynamic database in the top graph is close to the second sloshing frequency, which for this model is centered at 11.0 rad/s; the extrapolation curve is not properly fitted to the trend of the added mass. In the bottom graph, the maximum frequency of the hydrodynamic database is 13.0 rad/s, and the extrapolated values are much closer to the original data.