VM83

VM83
Impact of a Block on a Spring Scale

Overview

Reference:	F. P. Beer, E. R. Johnston, Jr., Vector Mechanics for Engineers, Statics and Dynamics, McGraw-Hill Book Co., Inc., New York, NY, 1962, pg. 531, problem 14.6.
Analysis Type(s):	Full Transient Dynamic Analysis (ANTYPE = 4)
Element Type(s):	Combination Elements (COMBIN40)
Input Listing:	vm83.dat

Test Case

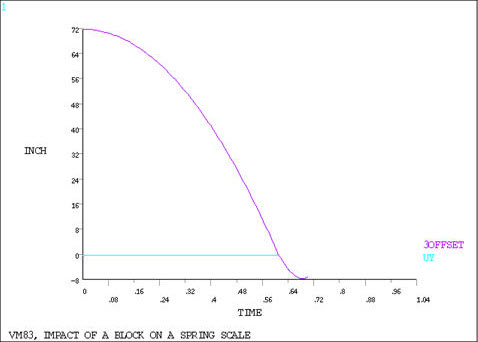
A block of weight W_B is dropped from a height h onto a spring scale pan of weight W_P. Determine the maximum deflection δ of the pan and the maximum fall of the block y. Assume the impact to be perfectly plastic as a theoretical approximation.

Figure 115: Spring Scale Problem Sketch

Material Properties

Geometric Properties

k₁ = 100 lb/in

W_B = 50 lb

W_P = 25 lb

h = 6 ft = 72 in

g = 386 in/sec²

Analysis Assumptions and Modeling Notes

The mass of the block (m_B) and the mass of the pan (m_P) are calculated as m_B = W_B/g = (50/386) lb-sec²/in and m_P = W_P/g = (25/386) lb-sec²/in respectively. Deflection of the pan due to gravity is W_P/k₁ = 0.25 in, hence the initial gap becomes (72-0.25) = 71.75 inches.

The spring length is chosen arbitrarily. The closed-gap spring constant (k₂ = 10,000 lb/in) is arbitrarily selected high enough to minimize the elastic contact effect but low enough to also allow a practical integration time step size. The integration time step (0.0005 sec) is based on < 1/30 of the period of the contact spring to minimize the numerical damping effect, and to allow the acceleration change to be followed reasonably well.

Automatic time stepping is used to reduce the total number of iterations needed to solve the problem. A static solution is done at the first load step to produce the initial pan condition before the start of the transient analysis. The maximum time of 0.7 sec allows the pan to reach its largest deflection.

To model the "plastic impact" a damper (C₂) is used which has the value of critical damping to prevent oscillation of the contact spring. Also, the two masses are locked together after initial contact by use of KEYOPT(1) = 1 on combination element type 1 (COMBIN40). Natural frequency of the closed gap is f₂ = sqrt(k₂m_p)/(2 π) = 62.54 Hz. Critical damping is calculated as C₂ = k₂/πf₂ = 10000 / (62.54 π) = 50.90 lb-sec/in. POST26 is used to extract results from the solution phase.

Results Comparison

Time = 0.689 sec	Target	Mechanical APDL	Ratio
Deflection, in	-7.7000	-7.6135	0.989
y, in	-79.450[1]	-79.414	1.000

Based on a perfectly plastic analytical solution.

Figure 116: Displacements of Block and Pan