VM25

VM25
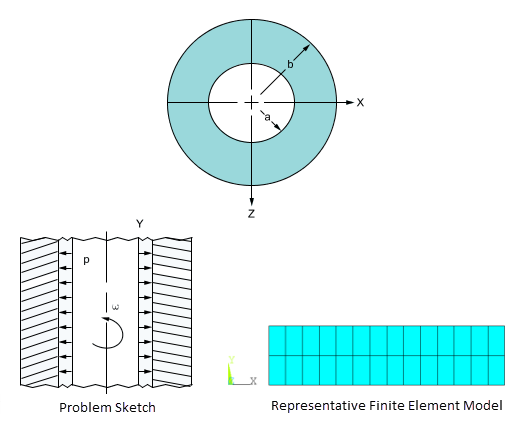
Stresses in a Long Cylinder

Overview

Reference:	S. Timoshenko, Strength of Material, Part II, Elementary Theory and Problems, 3rd Edition, D. Van Nostrand Co., Inc., New York, NY, 1956, pg. 213, problem 1 and pg. 213, article 42.
Analysis Type(s):	Static Analysis (ANTYPE = 0)
Element Type(s):	2D 8-Node Structural Solid Elements (PLANE183)
Input Listing:	vm25.dat

Test Case

A long thick-walled cylinder is initially subjected to an internal pressure p. Determine the radial displacement δ_r at the inner surface, the radial stress σ_r, and tangential stress σ_t, at the inner and outer surfaces and at the middle wall thickness. Internal pressure is then removed and the cylinder is subjected to a rotation ω about its center line. Determine the radial σ_r and tangential σ_t stresses at the inner wall and at an interior point located at r = X_i.

Figure 31: Long Cylinder Problem Sketch

Material Properties

Geometric Properties

E = 30 x 10⁶ psi

υ = 0.3

ρ = 0.00073 lb-sec²/in⁴

a = 4 inches

b = 8 inches

X_i = 5.43 inches

p = 30,000 psi

ω = 1000 rad/sec

Analysis Assumptions and Modeling Notes

The axial length is arbitrarily selected. Elements are oriented such that surface stresses may be obtained at the inner and outer cylinder surfaces.

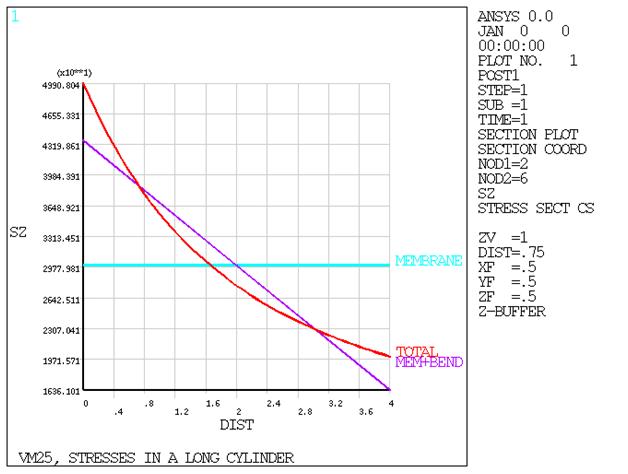
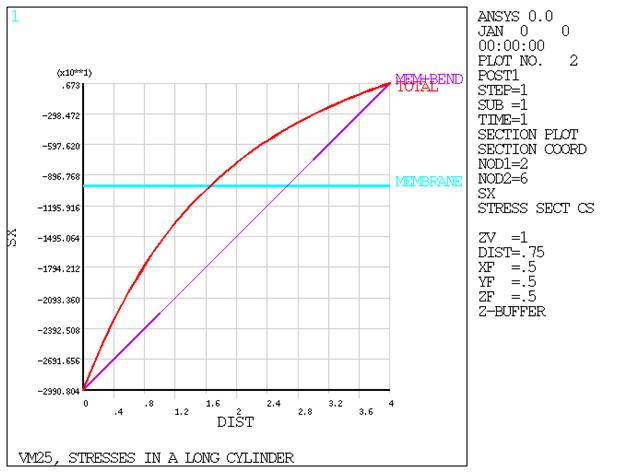
POST1 is used to display linearized stresses through the thickness of the cylinder when it is subjected to an internal pressure.

Results Comparison

		Target	Mechanical APDL	Ratio
p = 30,000 psi	Displacement_r, in (r = 4 in)	0.0078666	0.0078667	1.000
	Stress_r, psi (r = 4 in)	-30000.	-29908.046875	0.997
	Stress_r, psi (r = 6 in)	-7778.	-7757.541	0.997
	Stress_r, psi (r = 8 in)	0.	6.734	--
	Stress_t, psi (r = 4 in)	50000.	49908.046875	0.998
	Stress_t, psi (r = 6 in)	27778.	27757.541	0.999
	Stress_t, psi (r = 8 in)	20000.	19993.265	1.000
Rotation = 1000 rad/sec	Stress_r, psi (r = 4 in)	0.0	49.307	--
	Stress_t, psi (r = 4 in)	40588.	40526.285	0.998
	Stress_r, psi (r = 5.43 in)	4753.	4745.722	0.998
	Stress_t, psi (r = 5.43 in)	29436.	29406.567	0.999

Figure 32: SZ Stresses Along a Section (Internal Pressure)

Figure 33: SX Stresses Along a Section (Internal Pressure)