VM222

VM222
Warping Torsion Bar

Overview

Reference:

C-N Chen, "The Warping Torsion Bar Model of the Differential Quadrature Method", Computers and Structures, Vol. 66 No. 2-3, 1998, pp. 249-257.

Analysis Type(s):

Static Structural (ANTYPE = 0)

Element Type(s):

3D Linear Finite Strain Beam Elements (BEAM188)

3D Quadratic Finite Strain Beam Elements (BEAM189)

Input Listing:

vm222.dat

A cantilever I-beam is fixed at both ends and a uniform moment, M_x, is applied along its length.

Figure 365: Warping Torsion Bar Problem Sketch

Material Properties

Geometric Properties

Warping rigidity (EC_W) = 7.031467e12 Nmm⁴ and GJ=3.515734e7 Nmm²

Warping constant (C_W) =0.323e8 and J=431.979 (E=217396.3331684 N/mm² and G=81386.6878 N/mm²)

Poisson's Ratio = (E/(2*G))-1 = 0.33557673

b=40mm

h=80mm

t=2mm

L=1000mm

Moment = 1Nmm/mm

Figure 366: I-Beam Section Plot

Given that:

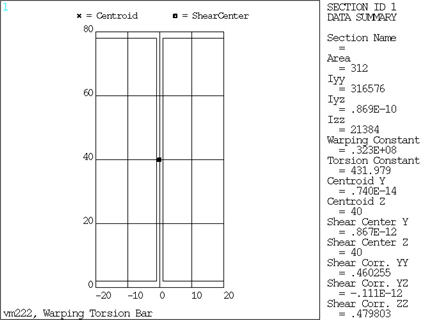
EC_w = 7.031467E12 Nmm⁴(warping rigidity)

Iyy = 316576 mm⁴ for this beam cross section

and

GJ = 3.515734E7 Nmm²

C_w = 0.323E8 mm⁶ (warping constant)

J = 431.979 mm⁴ (torsion constant)

E = 217396.333 N/mm² (Young's modulus)

Therefore υ = E/2G-1 = 0.33557673 (Poisson's ratio)

Uniformly distributed moments are converted to a moment load on each element.

mload1 and mload2 are the loads on the beam ends.

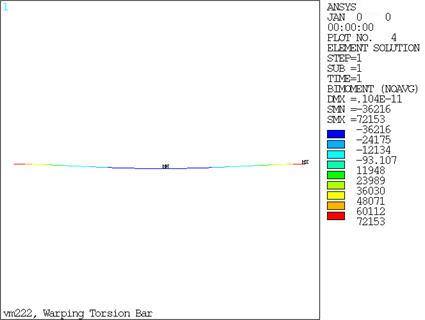
The warping DOF results are compared to the reference at the midspan.

MX Twist in X-Direction	Target	Mechanical APDL	Ratio
BEAM188	0.3293E-03	0.3326E-03	1.010
BEAM189	0.3293E-03	0.3330E-03	1.011

Figure 367: Warping Torsion Bar Plot

Figure 368: Warping Torsion Bar Plot