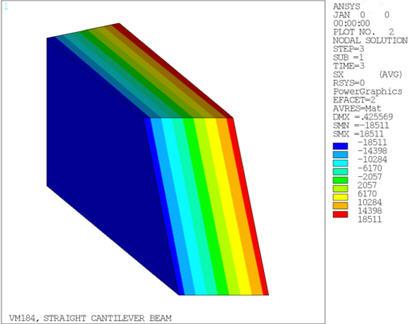
VM184

VM184
Straight Cantilever Beam

Overview

Reference:

Any Basic Mechanics of Materials Text

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

3D Coupled-Field Solid Elements (SOLID5)

3D 10-Node Tetrahedral Structural Solid Elements (SOLID92)

Tetrahedral Coupled-Field Solid Elements (SOLID98)

3D 10-Node Tetrahedral Structural Solid Elements (SOLID187)

Input Listing:

vm184.dat

Test Case

A beam of length , height h, and thickness t is built-in at one end and loaded at the free end with an axial force, an in-plane shear force and an out-of-plane shear force, all of magnitude F. Determine the deflections δ_x, δ_y, and δ_z at the free end due to these loads.

Figure 277: Straight Cantilever Beam Problem Sketch

Material Properties

Geometric Properties

E = 10 x 10⁶ psi

υ = 0.3

= 6 in

h = 0.2 in

t = 0.1 in

F = 1 lb

Analysis Assumptions and Modeling Notes

The problem is solved in four different ways:

using Coupled-Field Solid Elements (SOLID5)
using Tetrahedral Solid Elements (SOLID92)
using Tetrahedral coupled-Field Solid Elements (SOLID98)
using Tetrahedral Solid Elements (SOLID187)

POST1 is used to directly obtain the difference between the theoretical solution and the Ansys results in the form of a ratio, using the maximum displacement value on the free face.

Results Comparison

		Target	Mechanical APDL	Ratio
SOLID5	Deflection_x , in	3.000 x 10^-5	3.000 x 10^-5	0.993
	Deflection_y , in	0.10800	0.106830	0.989
	Deflection_z , in	0.43200	0.425536	0.985
SOLID92	Deflection_x , in	3.000 x 10^-5	3.000 x 10^-5	0.995
	Deflection_y , in	0.108000	0.106757	0.988
	Deflection_z , in	0.432000	0.425708	0.985
SOLID98	Deflection_x , in	3.000 x 10^-5	3.000 x 10^-5	0.995
	Deflection_y , in	0.108000	0.106757	0.988
	Deflection_z , in	0.432000	0.425708	0.985
SOLID187	Deflection_x , in	3.000 x 10^-5	3.000 x 10^-5	0.995
	Deflection_y , in	0.10800	0.106757	0.988
	Deflection_z , in	0.43200	0.425708	0.985

Figure 278: Element Display

Figure 279: Clipped and Capped Display of Stress Contours