VM136

VM136
Large Deflection of a Buckled Bar (the Elastica)

Overview

Reference:	S. Timoshenko, J. M. Gere, Theory of Elastic Stability, 2nd Edition, McGraw-Hill Book Co. Inc., New York, NY, 1961, pg. 78, article 2.7.
Analysis Type(s):	Static Analysis (ANTYPE = 0) with Large Deflection
Element Type(s):	3D 2 Node Beam (BEAM188)
Input Listing:	vm136.dat

Test Case

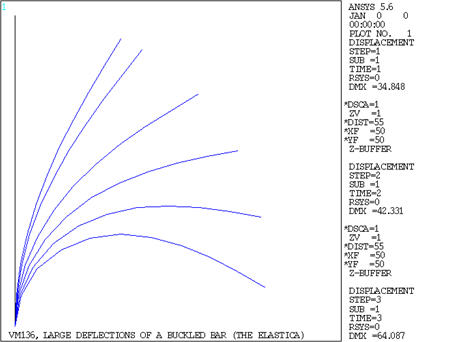
A slender square cross-sectional bar of length l, and area A, fixed at the base and free at the upper end, is loaded with a value larger than the critical buckling load. Determine the displacement (ΔX, ΔY, Θ) of the free end and display the deformed shape of the bar at various loadings.

Figure 189: Buckled Bar Problem Sketch

Material Properties

Geometric Properties

E = 30 x 10⁶ psi

= 100 in

width (w) = 0.5

height (h) = 0.5

F/F_cr = 1.015; 1.063; 1.152; 1.293; 1.518 and 1.884

Analysis Assumptions and Modeling Notes

The critical force, F_cr = π²EI/4 ² = 38.553 lb, is used for calculation of the applied load F.

A small perturbing force is introduced in the first load step to produce lateral, rather than pure compressive, motion. The number of equilibrium iterations for convergence increases significantly as the loading approaches the critical load (i.e. for solutions with Θ near zero). The six displacement solutions are overlaid by displaying with the /NOERASE option set.

Results Comparison

		Target	Mechanical APDL	Ratio
F = 44.413 lb Load Step 3	Angle, deg[1]	-60.0	-60.2	1.003
	DeflectionX, in	59.3	59.4	1.002
	DeflectionY, in	-25.9	-26.0	1.005
F = 49.849 lb Load Step 4	Angle, deg[1]	-80.0	-80.0	1.000
	DeflectionX, in	71.9	71.9	1.000
	DeflectionY, in	-44.0	-44.0	1.001
F = 58.523 lb Load Step 5	Angle, deg[1]	-100.0	-100.0	1.000
	DeflectionX, in	79.2	79.1	0.999
	DeflectionY, in	-65.1	-65.1	1.000
F = 72.634 lb Load Step 6	Angle, deg[1]	-120.0	-120.0	1.000
	DeflectionX, in	80.3	80.3	1.000
	DeflectionY, in	-87.7	-87.6	0.999

Angle (Θ) = ROTZ * (180/π ), where ROTZ is the node rotation in radians.

Figure 190: Deformed Shapes at Various Loads