VM130

VM130
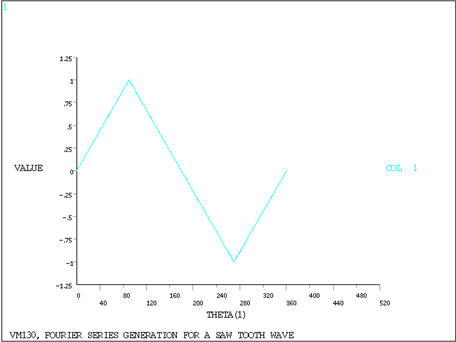
Fourier Series Generation for a Saw Tooth Wave

Overview

Reference:	S. Timoshenko, D. H. Young, Vibration Problems in Engineering, D. Van Nostrand Co., Inc., New York, NY, 1955, pg. 102, problem 2.
Analysis Type(s):	Fourier Coefficients Generated and Series Evaluated Using APDL
Element Type(s):	None
Input Listing:	vm130.dat

Test Case

For the saw tooth wave shown below, determine the coefficients of the Fourier series approximating this wave. Plot both the given wave and the wave as evaluated from the calculated series.

Figure 182: Saw Tooth Wave Problem Sketch

Analysis Assumptions and Modeling Notes

The wave is described by 121 points (arbitrary). Twenty four terms are assumed to be sufficient for the series. Since the wave is antisymmetric, only sine terms with odd modes are chosen.

Results Comparison

	Target	Mechanical APDL	Ratio
Mode 1 Coefficient	0.811	0.811	1.000
Mode 3 Coefficient	-0.901 x 10^-1	-0.902 x 10^-1	1.002
Mode 5 Coefficient	0.324 x 10^-1	0.326 x 10^-1	1.006
Mode 7 Coefficient	-0.165 x 10^-1	-0.167 x 10^-1	1.014

Figure 183: Fourier Display