Slide film damping occurs when surfaces move tangentially with respect to each other. Typical applications of slide film models are damping between fingers of a comb drive and damping between large horizontally moving plates (seismic mass) and the silicon substrate. Slide film damping can be described by a nodal force displacement relationship. FLUID139 is used to model slide film fluid behavior and assumes isothermal viscous flow.
Slide film problems are defined by:
(7–19) |
where:
| P = pressure |
| ν = plate fluid velocity |
| η = dynamic viscosity |
| z = normal direction of the laterally moving plates |
| t = time |
Slide film problems can be represented by a series connection of mass-damper elements with internal nodes where each damper represents the viscous shear stress between two fluid layers and each mass represents its inertial force. The damper elements are defined by:
(7–20) |
where:
| C = damping coefficient |
| A = actual overlapping plate area |
| di = separation between two internal nodes (not the gap separation) |
The mass of each internal node is given by:
(7–21) |
where:
| ρ = fluid density |
In case of slip flow boundary conditions (KEYOPT(3) = 1) the fluid velocity at the moving plate is somewhat smaller than the plate velocity itself. Slip flow BC can be considered by additional damper elements which are placed outside the slide film whereby the damping coefficient must be:
(7–22) |
where:
| Lm = mean free path length of the fluid at the current pressure |
In case of second order slip flow (KEYOPT(3) = 2) the damping coefficient is:
(7–23) |
where Kn is defined with Equation 7–10
Note that all internal nodes are placed automatically by FLUID139.
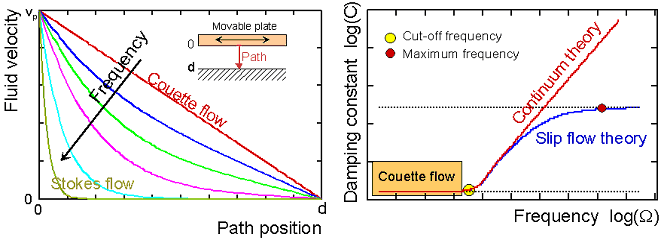
Two node models are sufficient for systems where the operating frequency is below the cut-off frequency which is defined by:
(7–24) |
where:
| fc = cut-off frequency |
| d = gap separation |
In this special case, damping coefficients are almost constant, regardless of the frequency, and inertial effects are negligible. At higher frequencies, the damping ratio increases significantly up to a so-called maximum frequency, which is defined by:
(7–25) |
where:
| fmax = maximum frequency |
The meaning of both numbers is illustrated below:
In case of large signal damping, the current overlapping plate are as defined by:
(7–26) |
where:
| Anew = actual area |
| Ainit = initial area |
| ui = nodal displacement in operating direction of the first interface node |
| un = nodal displacement of the second interface node |
For rectangular plates which move parallel to its edge, the area change with respect to the plate displacement (dA/du) is equal to the plate width. These applications are typical for micro-electromechanical systems as comb drives where the overlapping area changes with respect to deflection.