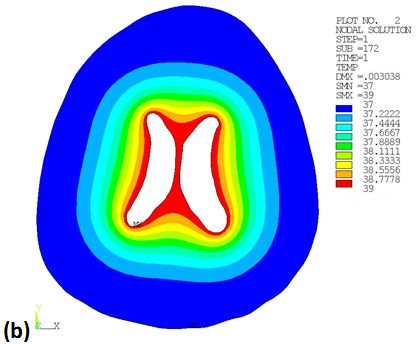
Heat transfers from the inner surface to the outer surface over time. Stepped loading is evident via the minimum and maximum temperatures.
Figure 50.2: Temperature Distribution Contour of Brain Cross-section at Time 0.02 (a) and Time 1 (b)
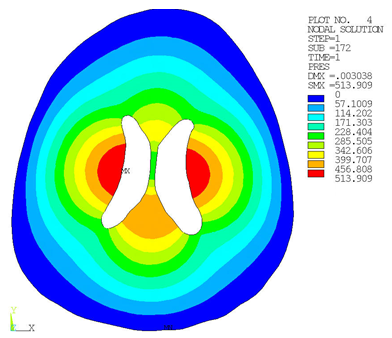
Pore-pressure distribution differs in some ways from the reference results:[1]
Several reasons account for the difference:
The formulation used in this simulation (intrinsic to the coupled pore-pressure-thermal elements) differs from that of the reference problem.
This simulation uses a hyperelastic material. The reference problem uses an elastic material.
The reference problem does not include thermal degrees of freedom.
The geometry in this simulation is captured using digitized points from the reference.
For the coupled pore-pressure-thermal elements, the mass-balance equation for the pore-fluid phase is:
where:
 = volumetric strain |
 = compressibility parameter |
 = thermal expansion coefficient |
 = temperature |
 = flow source |
In the reference problem, the mechanical equilibrium is:
In our problem, 
, 
, 
, and 
can be eliminated by appropriately defining the material property,
boundary conditions, and loadings. The term 
cannot be eliminated; therefore, the model used in this simulation and
the reference model can be inherently different. Generally, however, our simulation
gives reasonable pore-pressure distribution.
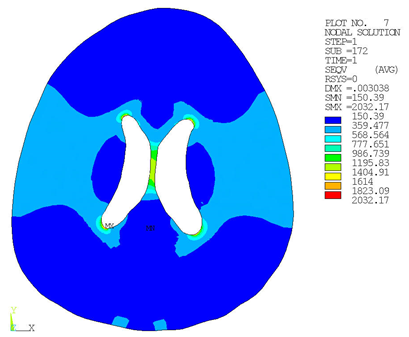
The stress field around the ventricle corners can be accurately calculated due to the mesh refinement around those areas:
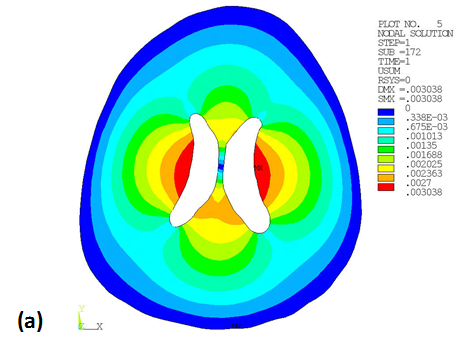
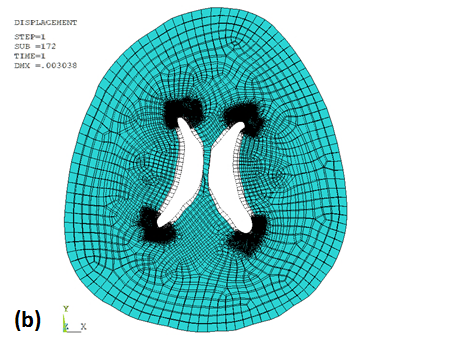
The maximum deformation concentrates around the ventricle:
