The model is a plain cylindrical journal bearing supporting a shaft rotating at 100000 rad/s. The stiffness and damping characteristics are calculated at the adimensional equilibrium position XX = 0.5, YY = -0.7, and XXdot = YYdot = -0.05.
The bearing properties are as follows:
| Clearance: 1 x 10-4 m |
| Length: 0.02 m |
| Radius: 0.01 m |
| Viscosity: 0.07 Pa·s |
A perturbation increment of 1 x 10-5 is used.
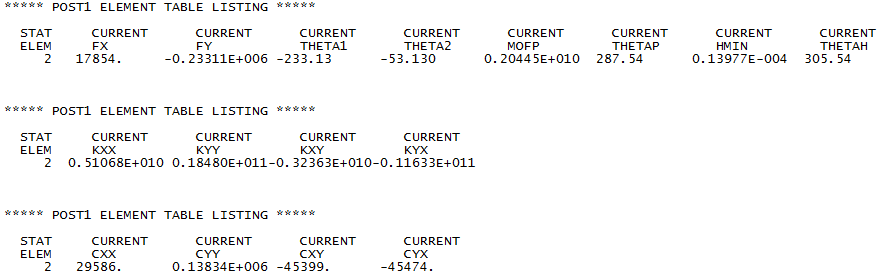
! ** Bearing parameters mass = 1 ! unused xclear = 1e-4 length = 0.02 radius = 0.01 mu = 0.07 omegaj = 1e+5 pertInc = 1e-5 ! ** Equilibrium position (adimensional) XX = 0.5 YY = -0.7 XXdot = -0.05 YYdot = -0.05 u1 = XX*xclear u2 = YY*xclear veloc1 = XXdot*xclear*omegaj veloc2 = YYdot*xclear*omegaj /prep7 ! ** Nodes n, 1, -1 n, 2, 0 ! ** Elements et, 1, 21,,, 2 ! 3D no rotary inertias r, 1, mass et, 2, 214 keyopt,2,1, 2 ! Reynolds integration r, 2, xclear, length, radius, veloc1, veloc2, pertInc ! ** Material mp,visc,2, mu ! ** Mesh type,1 real,1 e, 2 type,2 real,2 mat,2 e, 1, 2 ! ** Boundary conditions d, all, all, 0.0 ddel, 2, UX ddel, 2, UY finish ! ** Static analysis with specified displacements /solu antype, static omega,,, omegaj d,2,ux, u1 d,2,uy, u2 outres,all,all solve finish /post1 set,last esel,,elem,,2 etable, fx, smisc,1 etable, fy, smisc,2 etable, theta1, nmisc,1 etable, theta2, nmisc,2 etable, mofp, nmisc,3 etable, thetap, nmisc,4 etable, hmin, nmisc,5 etable, thetah, nmisc,6 pretab etable, kxx, nmisc,7 etable, kyy, nmisc,8 etable, kxy, nmisc,9 etable, kyx, nmisc,10 pretab, kxx, kyy, kxy, kyx etable, cxx, nmisc,11 etable, cyy, nmisc,12 etable, cxy, nmisc,13 etable, cyx, nmisc,14 pretab, cxx, cyy, cxy, cyx finish