*FFT

*FFT, Type, InputData, OutputData, DIM1, DIM2, ResultFormat
Computes the fast Fourier transformation of a specified matrix or vector.

APDL: Matrix Operations

Argument Descriptions

Type

Type of FFT transformation:

FORW --: Forward FFT computation (default).
BACK --: Backward FFT computation.

InputData

Name of matrix or vector for which the FFT will be computed. This can be a dense matrix (created by the *DMAT command) or a vector (created by the *VEC command). Data can be real or complex values. There is no default value for this argument.

OutputData

Name of matrix or vector where the FFT results will be stored. The type of this argument must be consistent with InputData (see table below). There is no default value for this argument.

FFT Domain	Forward		Backward
FFT Domain	Input Data	Output Data	Input Data	Output Data
Real	Real	Complex	Complex	Real
Complex	Complex	Complex	Complex	Complex

DIM1

The number of terms to consider for a vector, or the number of rows for a matrix. Defaults to the whole input vector or all the rows of the matrix.

DIM2

The number of columns to consider for a matrix. Defaults to all the columns of the matrix. (Valid only for matrices.)

ResultFormat

Specifies the result format:

FULL --: Returns the full result. That is, the result matches the dimension specified on this command (DIM1, DIM2).
PART --: Returns partial results. For real input data, there is a symmetry in the results of the Fourier transform as some coefficients are conjugated. The partial format uses this symmetry to optimize the storage of the results. (Valid only for real data.)

Notes

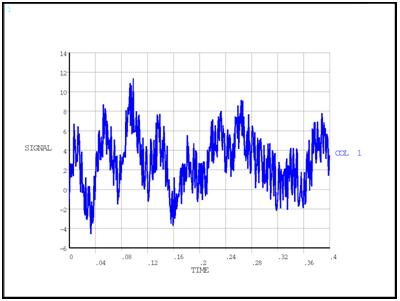
In the example that follows, the fast Fourier transformation is used to filter frequencies from a noisy input signal.

Example Usage

The fast Fourier transformation can be used to create a filter to remove noise from a noisy input signal.

Figure 4: Input Signal

The input signal is decomposed in the Fourier space using the *FFT,FORW command so that the frequencies that compose the signal can be observed.

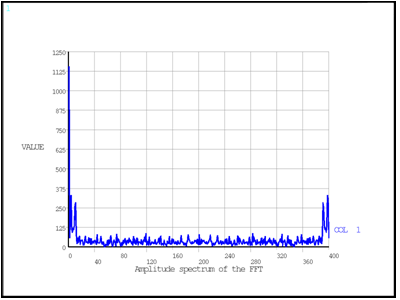
Figure 5: Amplitude Spectrum of the FFT

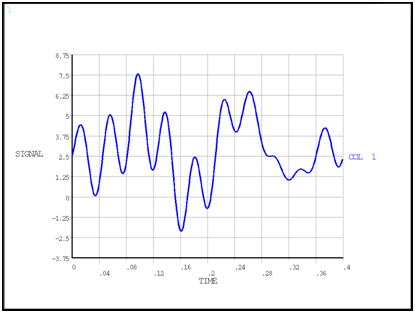
The filter applies a threshold on the Fourier coefficients. Fourier coefficients of small amplitude are the result of the noise in the input signal. Only coefficients of a large amplitude are significant. The inversion of the *FFT command (*FFT,BACK command) rebuilds the signal from the remaining coefficients.

Figure 6: Signal Obtained with the Filter

Example input demonstrating *FFT usage is provided below:

/com,*************************************************
/com,*  Usage example of the *FFT APDLMath command.  *
/com,*  Use FFT to filter a noisy sinusoidal signal. *
/com,*************************************************
/verify
/nopr

/post26

/gopr
/com, *** Definition of the parameters for the signal

pi             = acos(-1)
periode1       = 2*pi/40.0
phase1         = 4.0
amplitude1     = 2.5
periode2       = 2*pi/150.0
phase2         = 0.0
amplitude2     = 2.0
periode3       = 2*pi/140.0
phase3         = 0.0
amplitude3     = 1.5
amplitudenoise = 6.0
n              = 400       !number of points in the sampling input signal
tbegin         = 0.0       !start time for the signal
dt             = 0.001     !time step
tend           = tbegin + (n-1)*dt


/com, *** Definition of the parameters

threshold = 150.0
FFTmethod = 1 !0 = FFT giving partial results , 1 = FFT giving full results


/com, *** Create a signal from two sinus and add noise

*dim,signal,array,n
*dim,t,array,n
*dim,noise,array,n
*vfill,noise,rand

omega1 = (2.0*pi) / periode1
omega2 = (2.0*pi) / periode2
omega3 = (2.0*pi) / periode3

*do,ii,1,n
  noisec     =  amplitudenoise * noise(ii)
  tc         =  tbegin + (ii-1)*dt
  t(ii)      =  tc
 signal(ii) = amplitude1*sin(omega1*tc+phase1) + amplitude2*sin(omega2*tc+phase2) + amplitude3*sin(omega3*tc+phase3) + noisec
*enddo


/com, *** Display the input signal

*dim,signaldisp,table,n
*dim,tdisp,table,n

*do,ii,1,n
   tdisp(ii)=t(ii)
   signaldisp(ii)=signal(ii)
*enddo

/show,png
/AXLAB,X,TIME
/AXLAB,Y,SIGNAL
/color,curve,BLUE
/color,grbak,WHIT
/color,wbak,WHIT
/color,axes,BLAC
/color,axlab,BLAC
/color,axnum,blac
/GROPT,FILL,OFF
*vplot,tdisp,signaldisp


/com, *** Copy signal in an APDLMath vector

*vec,sigvec,d,alloc,n,1
*do,ii,1,n
 sigvec(ii) = signal(ii)
*enddo


/com, *** Perform a Fast Fourier Transform

*vec,VFFT,Z,ALLOC,n,1
*if,FFTmethod,eq,0,then
  *FFT,FORW,sigvec,VFFT,,,PART   !partial FFT (use symmetry properties)
*else
  *FFT,FORW,sigvec,VFFT,,,FULL   !full FFT
*endif  


/com, *** Determine the real part and the imaginary part of the Fourier's coefficients

*vec,VFFTI,Z,COPY,VFFT
*AXPY,,,,0.,-1.,VFFTI
*vec,VI,D,COPY,VFFTI
*vec,VR,D,COPY,VFFT


/com, *** Compute the modulus of the Fourier's coeff

*EXPORT,VR,APDL,fftr
*EXPORT,VI,APDL,ffti

sizeVR = VR_rowDim

*if,FFTmethod,eq,0,then
  sizeVR = sizeVR/2
*endif

*dim,ind,table,sizeVR
*dim,modfft,array,sizeVR

*do,ii,1,sizeVR
  ind(ii)   = ii
  modfft(ii)= sqrt( fftr(ii)*fftr(ii) + ffti(ii)*ffti(ii) )
*enddo


/com,*** Display the Amplitude spectrum of the FFT

*dim,modfftdisp,table,sizeVR
*do,ii,1,sizeVR
   modfftdisp(ii) = modfft(ii)
*enddo

/show,png
/AXLAB,X,Amplitude spectrum of the FFT
/AXLAB,Y,
*vplot,ind,modfftdisp
fini


/com, *** Threshold on Fourier coefficients

*print,VR
*do,ii,1,sizeVR
  module = modfft(ii)
  *if,module,lt,threshold,then
    VR(ii) = 0.0
    VI(ii) = 0.0
  *endif
*enddo


/com, *** Invert Fourier Transform

*vec,VIFT,Z,COPY,VR
*AXPY,0.0,1.0,VI,1.0,0.0,VIFT
*vec,VFILTER,D,ALLOC,VR_DIM

*FFT,BACK,VIFT,VFILTER


/com, *** Display the filtered signal

*EXPORT,VFILTER,APDL,filterSignal
*dim,fsignal,table,sizeVR

*do,ii,1,sizeVR
   fsignal(ii) = filterSignal(ii)
*enddo

/show,png
/AXLAB,X,TIME
/AXLAB,Y,SIGNAL
*vplot,tdisp,fsignal
fini

/com, *** Free the APDLMath objects
*free,all

Menu Paths

This command cannot be accessed from a menu.