Use the SEMIIMPLICIT command to activate the semi-implicit method:

SEMIIMPLICIT, Option, Type, Value

Use the Option field to specify various controls for the semi-implicit solution (see the SEMIIMPLICIT command for a list of valid Option values). Issue the command multiple times to specify the various controls, or issue the command once with no arguments to activate the semi-implicit method using default settings (see the command description for default values). The command is valid only in the solution processor (/SOLU) and must be issued before the first SOLVE command.

The following two Option values are most often used:

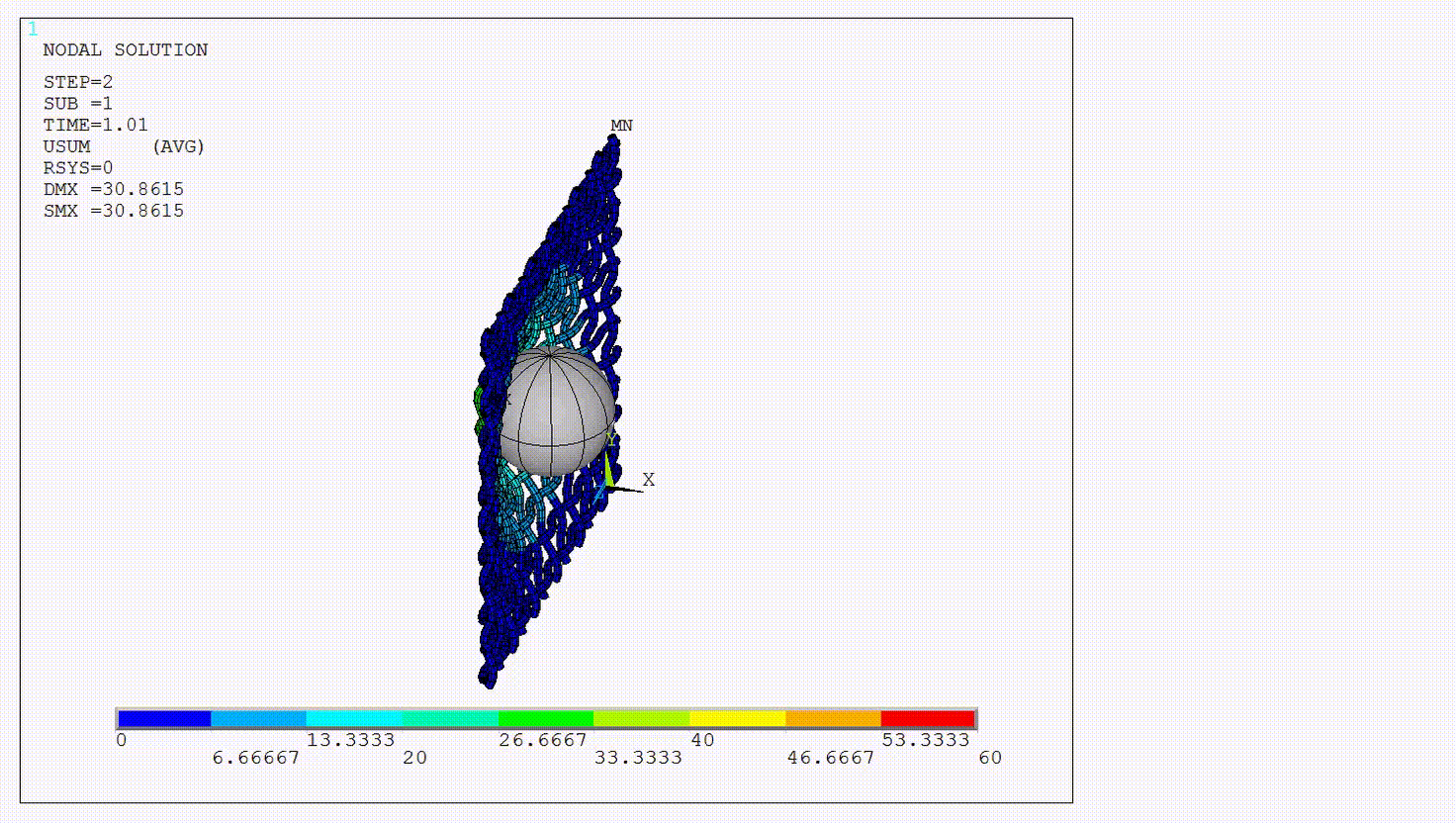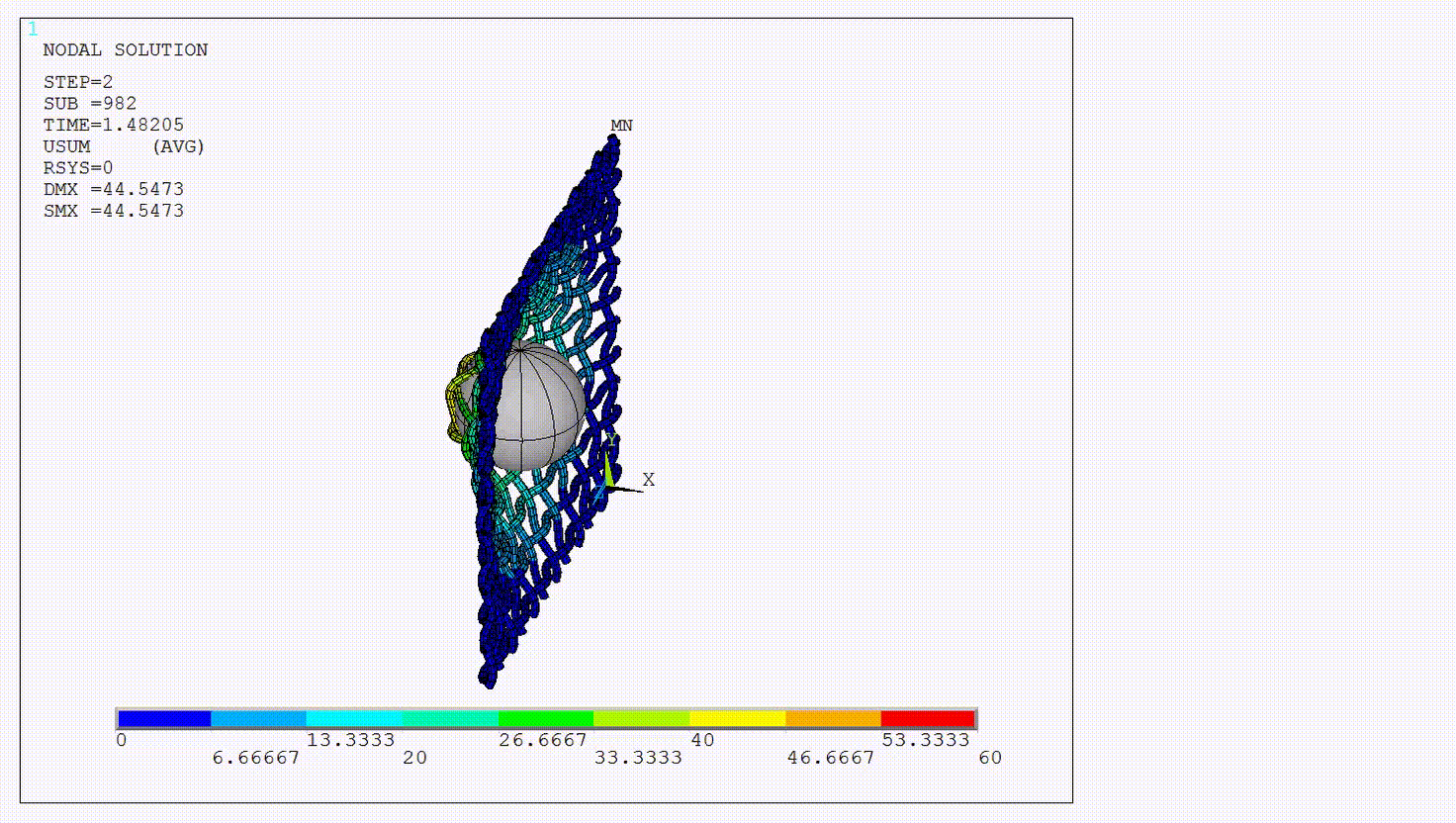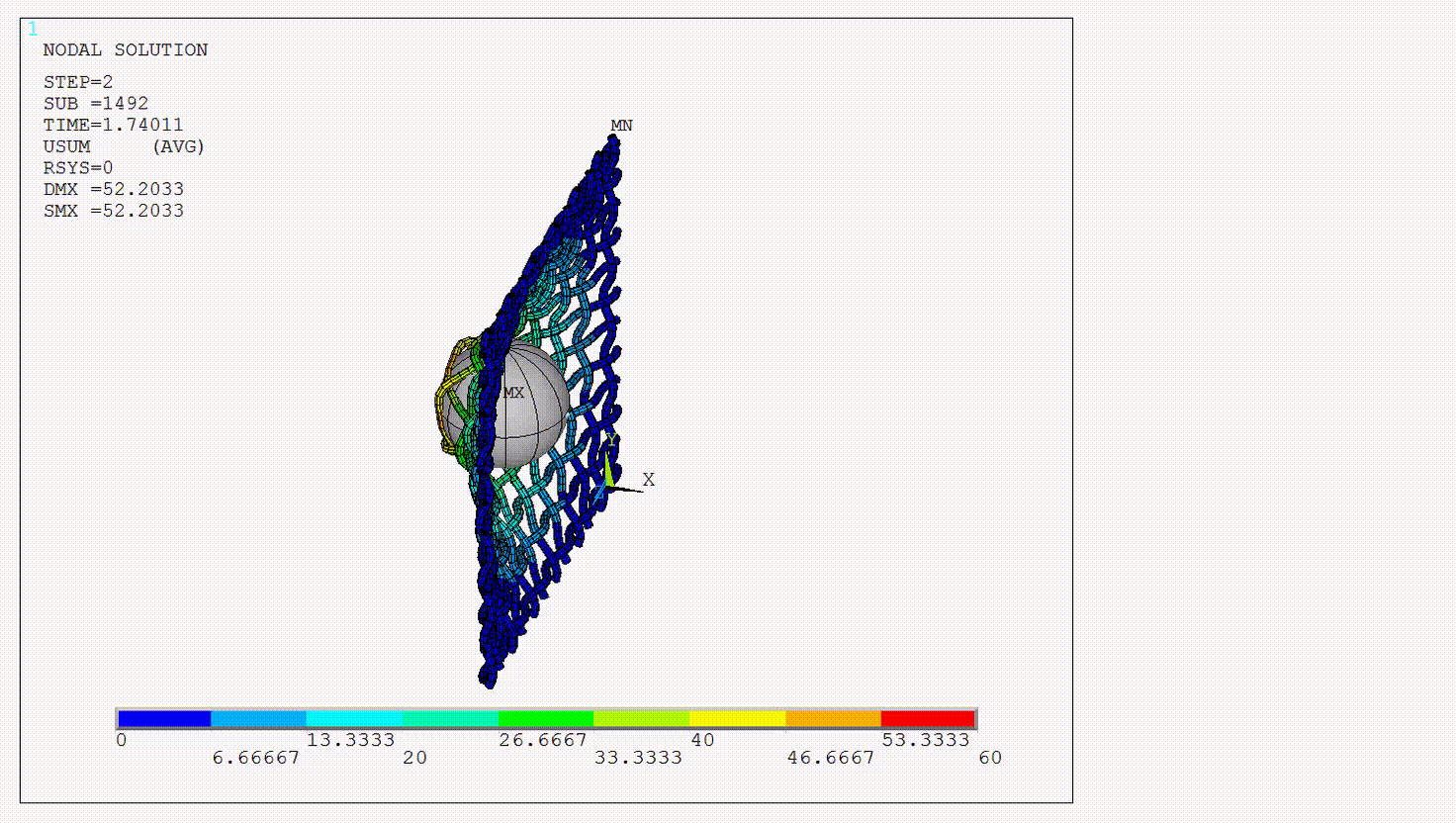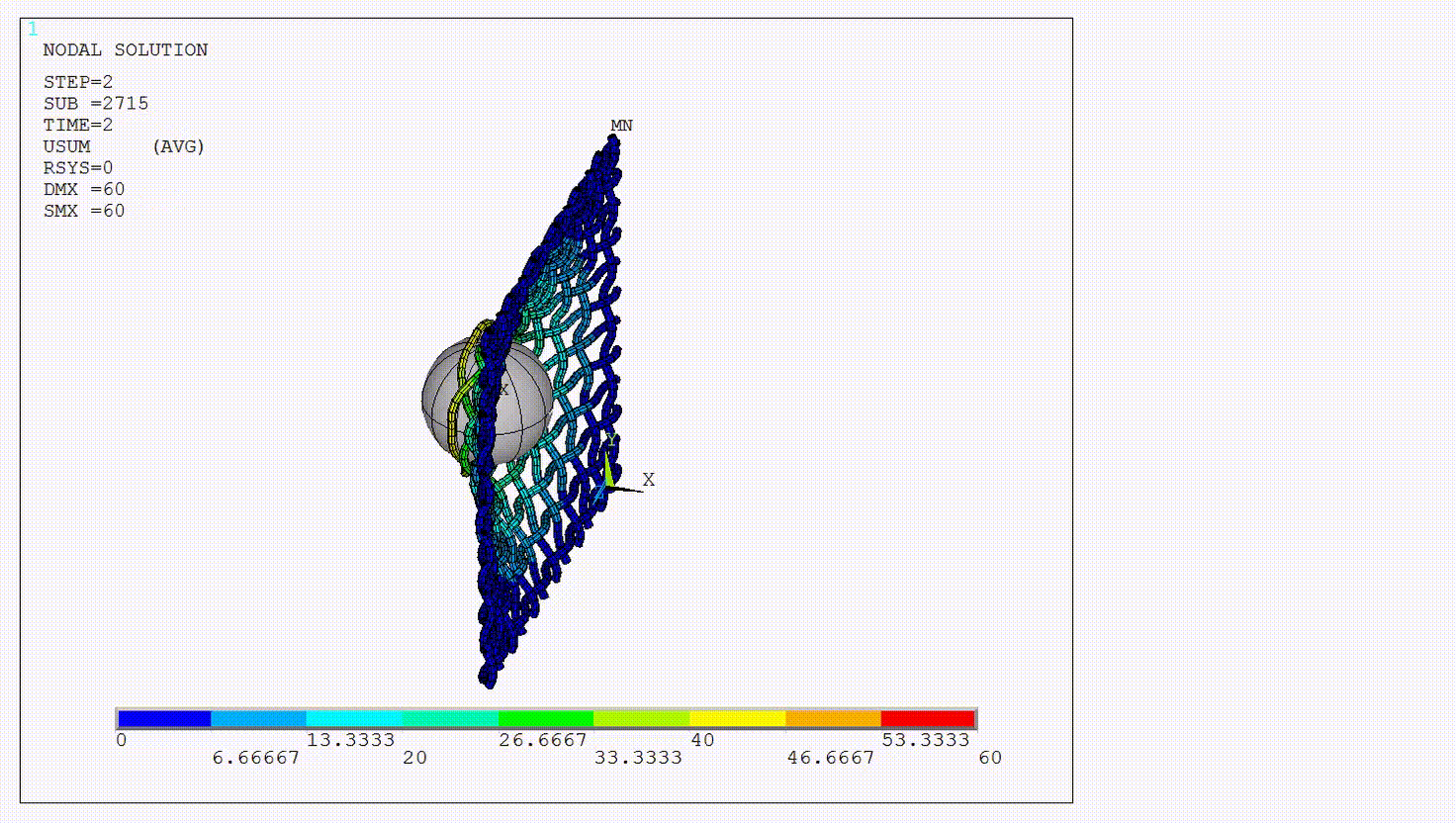
To illustrate use of this command and the basic semi-implicit procedure, the solution procedure is explained with respect to a representative example. The figure below shows a rigid ball impacting a net modeled by beam elements.

Figure 2.1: Semi-Implicit Example Model

A purely implicit solution could have difficulty converging for this model due the highly nonlinear nature of the analysis. It is therefore a good candidate for the semi-implicit method. Only two SEMIIMPLICIT commands are needed beyond the typical input:

semiimplicit,msca,dtim,1/5000    ! Use a selective mass scaling factor such that the semi-implicit 
                                 ! solution phase uses time increments of the order 1/5000
semiimplicit,etoi,time,0.1       ! Time to spend in the semi-implicit phase is 0.1

The different phases of the semi-implicit method are described below.

Initial Implicit Solution Phase

The solution starts off as an implicit static analysis. The SEMIIMPLICIT command enables the solver to switch to the semi-implicit solution method when the implicit method fails to converge. The transition is noted in the output as follows:

>>> TRANSITIONING TO SEMI-IMPLICIT METHOD

Semi-Implicit Solution Phase

During the semi-implicit solution phase, Newton-Raphson iterations are not required and each substep has only one iteration. The resulting solution is checked for several possible errors, including but not limited to sudden jumps in the displacement increment, an invalid mesh, an invalid contact solution, and an invalid material state. The substep is bisected by reducing the time increment of the invalid substep. During the semi-implicit solution phase, 10 bisections are allowed and the minimum time increment is set to (total step time)/1x10¹⁵. Some of the element level error checks that trigger bisection in an implicit solution phase are completely ignored.

Since the semi-implicit method has only one iteration per substep, the solution for a substep may not be stable (that is, it may violate some of the element level error checks). However, this is only apparent when element calculations are done in the next substep. When there is an element error and bisection is performed, the program recalculates the previous completed substep with a smaller time increment by resuming the previous substep, which is saved in the file Jobname.psav. The previous subtep results, if written in the Jobname.rst file, are deleted as well, and new results are written if the substep completes successfully. Similarly, the restart file for a substep is written after the end of the next substep to make sure that the solution of the substep does not produce element errors in the next substep.

During the semi-implicit solution, the kinetic energy and potential energy are printed out instead of solution residual norms that are printed during the implicit phase. For example, in the solution output you will see something like this:

    Kinetic Energy =  745.8        Potential Energy = 0.8909E+06

When solving a quasi-static problem, the ratio of the kinetic to potential energy is a good indicator of how close the semi-implicit dynamic solution is to a quasi-static analysis. As a rule of thumb, kinetic energy should be < 1% of potential energy. Reducing the mass scaling and/or reducing the factor of safety can help to keep the kinetic energy low.

The monitor file (file.mntr) automatically lists the total kinetic and potential energies under variables 2 and 3 whenever a semi-implicit solution is activated. If you explicitly input the MONITOR command to monitor variables, the command you input takes precedence and the energies are not printed.