标准面(Standard)

球面是最常用的光学面型。球面的球心在当前的光轴上，球面顶点也在当前的光轴位置上。 OpticStudio 把平面当作球面的特例（曲率半径为无穷大的球面），同时把圆锥面也当作特例。标准面的"矢高"或z坐标值由下式给出

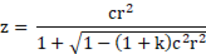
其中c是曲率（半径的倒数），r是以镜头单位表示的径向坐标，k为圆锥系数。其中圆锥系数小于-1时为双曲面，等于-1时为抛物线，在-1和0之间时为椭圆，等于0时为球面，大于0时为扁椭圆面。

关于圆锥系数的更多信息，请参阅"镜头设计参考(References on Lens Design)"。

标准面不使用任何参数值。

用标准面模拟椭圆面(Modeling an ellipse with the standard surface)

这里有几个较方便的公式可以把椭圆面的半长轴和半短轴的长度转化为使用半径和圆锥系数进行描述。如果"a"为长半轴长度，"b"为短半轴长度，则

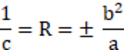
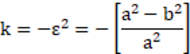
请参阅"双锥体(Biconic)"查看在x和y上具有不同半直径的椭圆面。

用标准面模拟轴锥镜(Modeling an axicon with the standard surface)

标准面可以用于创建一个几乎完美的轴锥镜。如果(1+k)c²r²>>1，则标准面减化至

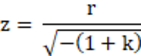
或z = rtan(α)，其中

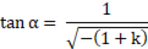
且α是轴锥角，从XY平面到轴锥镜表面测量得到。要创建一个轴锥镜，从描述的角(α)计算圆锥系数值(k)，并使用任何小的值作为曲率半径。k的结果必须为负数。半径或曲率的确切值不重要，只要大约是小于轴锥镜径向孔径的三个或更高数量级。虽说某种意义上轴锥镜在原点无尖端时不完美，但这里表面顶点周围的区域将以某一半径圆形近似给出。这样表面在各个区域都是光滑的，事实上光线追迹也需要这样的特性。但是，近轴数据，例如有效焦距、近轴放大率和其它常见的一阶光学性质，它们对轴锥镜表面来说通常没有意义。尽管面的形状依然是圆锥非球面，但由轴锥镜形状得到的系统近轴特性不能代表整个光学表面。在这种情况下，只用曲率半径就不能很好地描述光学表面。

下一部分：

• 超圆锥面(Superconic)