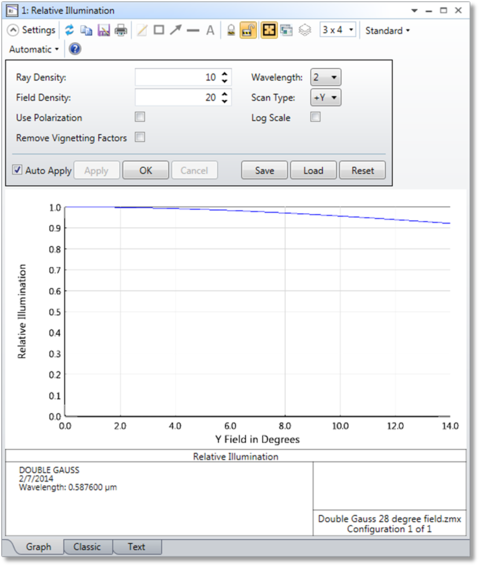
相对照度(Relative Illumination)
"相对照度"分析可计算均匀朗伯场景的径向视场坐标变化的相对照度。此功能还可以计算有效F/#。
光线密度(Ray Density) 对出瞳照度积分所使用的光线阵列一侧的光线数量。若值为10,将追迹大约10 x 10 x pi / 4或78条光线。更高的光线密度可得出更准确的结果,但要以更长的计算时间为代价。光线密度最小值是5。
视场密度(Field Density) 径向视场坐标上要计算其相对照度的点的数量。视场密度越大,生成的曲线越平滑。
使用偏振(Use Polarization) 如果选中,则考虑偏振。有关如何定义偏振态以及如何通过分析功能使用偏振的信息,请参阅"偏振(系统选项)(Polarization (system explorer))"。
除去渐晕因子(Vignetting Factors) 如果选中,则自动除去渐晕因子。请参阅"FFT MTF vs 视场"说明中的"关于渐晕因子的注解(Comment about vignetting factors)"。
波长(Wavelength) 选择用于计算的波长。相对照度是单波长实体。
扫描类型(Scan Type) 选择+y、+x、-y或-x视场扫描方向。
对数缩放(Log Scale) 如果选中,将显示对数缩放而非线性缩放。
详述(Discussion)
此功能可计算随径向y视场坐标变化的相对照度(RI)。RI被定义为像面单位区域的照度强度,可归一化为视场中照度最大的点的照度(可能不在轴上)。计算需考虑切趾、渐晕、孔径、图像和光瞳的像差、F/#变化、色差、像面形状、入射角以及(可选)假设无偏振光的偏振效应。有关此方法基于的计算说明,请参阅M. Rimmer, "Relative illumination calculations", Proc.SPIE Vol. 655, p99 (1986)。发布的方法经扩展包括切趾、透射、偏振和非平面像面效应。计算方法假设以下条件都成立:
- 1.物体场景是水平均匀的朗伯面。
- 2.像面是物面的合理共轭面(即图像),因此物面的小光斑发出的光线可在像面上形成光斑图像。可存在像差,但光线应合理分布到像面上。
- 3.出瞳不能过于接近像面。如果F/#大于0.1并且光线像差比出瞳距离小,则符合此条件。
- 4.余弦空间像差不能过大以致在角空间中形成焦散面。角空间中的焦散面是指,入瞳不同部分的光线在像空间中的角度均相同。要检查这一点,请使用点列图功能中的"方向余弦(Direction Cosines)"选项(参阅"标准点列图(Standard Spot Diagram)"分析)。
通过对从图像点看到的出瞳有效区域积分,可计算相对照度。可使用图像余弦空间中的均匀网格在方向余弦空间中进行积分。
注意:RI计算通常不会生成余弦四次方曲线,因为所谓的余弦四次方"定律"实际是一种基于有光阑面的薄缓无像差透镜的近似。对于更通用的透镜,包括远心、像差或渐晕透镜,可以使用投射的实体角度或从图像位置看到的出瞳有效区域的积分计算RI,并且此计算不会生成简单的余弦四次方曲线。如果系统违背了计算假设,将显示错误消息,并且不会计算RI。
有效F/#(Effective F/#)
相对照度数据的文本列表还包含有效F/#的数据。有效F/#是具有100%透过率和圆形出瞳的完美光学系统为提供与所评估系统相同的图像照度所需要的F/#。有效F/#的计算公式是:
其中A是为系统透过率加权的余弦空间中光瞳的投射实体角度区域。有效F/#是一个有用的指标,可用于比较不同光学系统所形成的图像的亮度,因为该指标会考虑RI,并且不依赖于孔径形状。有关更多信息,请参阅"F-Number and the radiometry of image forming optical systems with non-circular aperture stops," R. Siew, Proc. of SPIE Vol. 5867 (2005)。
下一部分:


