全息面1(Hologram 1)
全息面l可用来模拟光学构造的全息元件。全息面可以是平面、球面或圆锥面,且全息面之后的介质可以是空气或玻璃。玻璃也可以是"反射面(Mirror)",以指定全息面是构造且用于反射。全息元件本身通过两个不同构造点的x、y、z坐标、构造波长和衍射级次来描述。全息元件根据下述方程对光程的偏离进行计算:
其中,nˆ是在光线交点处垂直于全息面的单位矢量,ro是沿着第一条构造光束的单位矢量,rr是沿着第二条构造光束的单位矢量,r’r是沿着入射读出光束的单位矢量,r’o为折射光线,λc和λp为构造波长和重现波长,m为衍射级次。m=0表示光线不偏离,而m的其它整数值表示较高的衍射级次。这里用到的符号引用自(1986年)Welford编写、Adam Hilger出版的《Aberrations of Optical System》一书。模拟全息面需要理解它的原理和特性,这超出了本参考手册的范围,建议用户在使用此功能前先参阅Welford的书及其它一些参考书目。
大多数全息元件的构造和使用都应用于透射或反射中。也有应用是先构造全息元件用于透射,然后把基底镀铝再用于反射。在这种特殊情况下,可以使用指定了负构造波长的全息面来模拟。尽管在这种情况下光线追迹是正确的,但OPD追迹将无法起作用。
默认情况下,OpticStudio只能模拟全息元件对光程的偏离影响。对于效率等其它属性,必须使用Volume Hologram?参数将表面设置为体全息图。
两束构造光束可用各自的点光源进行定义。点光源的x、y、z坐标是相对于全息面顶点坐标测量得到,以镜头单位表示。 OpticStudio 用两束构造光束的局部坐标和构造点数据来计算在光线与面交点处的单位矢量。构造波长的单位为微米。如果到点光源的距离大于1.0E+08镜头单位,则假设点在无限远处,且构造光束是该点发出的完美平面波。这种假设比简单输入大坐标值能获得更精确的OPD计算。
要将全息面1用作体全息图,请设置体全息图(Volume Hologram)? 这允许输入下列体全息图参数。
用两个指定的构造光束之间的干涉来定义全息面,假定构造光束无像差。可以使用一般方法来模拟有像差构造光束光学制造全息面,参见"光学制造全息(Optically Fabricated Hologram)"。
可以使用"光学制造全息"面对有像差构造光束形成的光学构造全息面进行模拟。
全息面1假设两束构造光从指定的构造点发散开来。由于构造光束光路可逆,因此也相当于两构造光束向构造点会聚。有些全息构造方法要求一束为会聚光而另一束为发散光。如需了解有关这类全息面的信息,请参考"全息面2(The Hologram 2 surface)"。
关于考虑全息面两侧材料折射率的注解
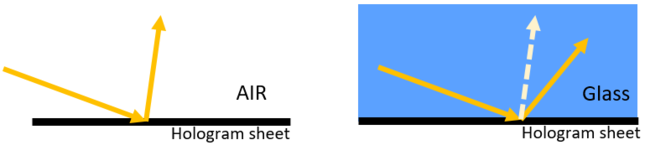
我们上面讨论的方程没有考虑全息表面两侧材料的折射率。 如果其中一条光线来自不同的材料,那么我们应该将它的单位矢量乘以光线所在位置的折射率。例如,如果全息图附加在折射率为ng并用于反射的玻璃上,那么我们应该将入射读出光束和折射光束写为ngr'r和ngr'o。这会由OpticStudio进行处理。但是,始终假设构造光束位于空气中,因为没有用于定义构造光束所在材料的折射率的参数。 假如全息图由非空气材料光学构造而成,构造波长应有效地从λc变为λc/ng。
请注意,根据我们上面讨论的内容,当全息图两侧的材料折射率不同时,我们应该预期光线会衍射到不同的方向。这正是我们对光栅衍射的期望。 下面显示的是描述这个概念的草图。
全息面1的参数定义(参数14-21仅在参数13 ≠ 0时可用)
| 参数# | 定义 |
| 1 | 第一束构造光束的X坐标,Construct X1 |
| 2 | 第一束构造光束的Y坐标,Construct Y1 |
| 3 | 第一束构造光束的Z坐标,Construct Z1 |
| 4 | 第二束构造光束的X坐标,Construct X2 |
| 5 | 第二束构造光束的Y坐标,Construct Y2 |
| 6 | 第二束构造光束的Z坐标,Construct Z2 |
| 7 | 构造波长,λc |
| 8 | 衍射级次,m |
| 13 | 体全息图?(用0表示False,用1表示True) |
| 14 | 全息图厚度(仅用于效率计算而非光线追迹) |
| 15 | 构造光束1在全息图外看到的折射率,n1 |
| 16 | 构造光束2在全息图外看到的折射率,n2 |
| 17 | 全息乳剂的平均折射率,n |
| 18 | 折射率调制,dn |
| 19 | 收缩率(用0表示无收缩,否则为厚度比例,例如0.98是2%的收缩率) |
| 20 | 折射率偏移(Index Shift)(显影后平均折射率的变化) |
| 21 | 考虑菲涅尔面(Fresnel)?(用0表示False,用1表示True) |
下一部分:


