トロイダル
トロイダル面は、Y-Z 平面で曲線を定義し、Y 軸に平行で Z 軸と交差する軸を基準に、この曲線を回転させることで形成されます。トロイダルは Y-Z 平面の曲率の基円半径と、コーニック定数および多項式非球面係数を使用して定義します。Y-Z 平面の曲線は、以下の式で定義されます。
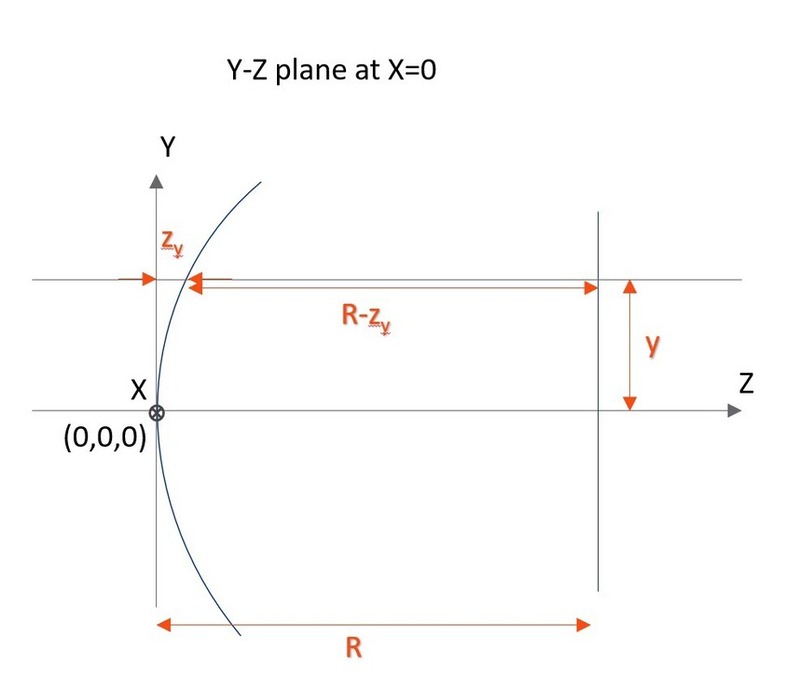
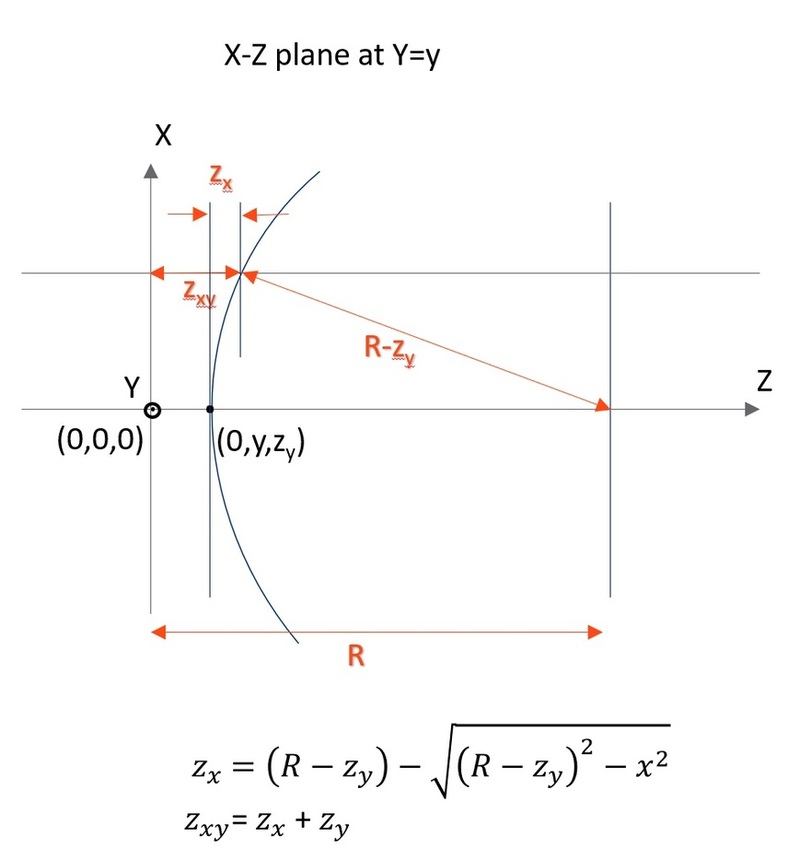
この曲線は偶数次非球面サグの式に似ていますが、16 次の項が省略され、座標の引数が r ではなく y になっています。次に、この曲線は、頂点から距離 R の位置で、軸を基準に回転します。この距離 R は回転の半径を指しており、正または負の数になります。曲率の Y-Z 半径は、スプレッドシート エディタで標準面の半径と同じ列で指定します。回転の半径は、パラメータ列番号 1 で設定します。X 方向に平らなシリンダ レンズをモデル化するにはゼロを使用します。OpticStudio はこれを無限半径と解釈します。
以下のゼルニケ標準サグの項を追加することで、オプションで面を変更できます。
ここで zt は基本のトロイダル サグです。ゼルニケ標準の項は「ゼルニケ標準サグ」のセクションで定義されているとおりで、レンズ データ エディタの [インポート] (Import) セクションを使用して入力します。Y-Z 半径が無限に設定されている場合は、x 方向には屈折力があるが y 方向にはない平面を記述可能なので、シリンダはどちらの方向にも向く可能性があります。その他のパラメータ列は、次の表に示すように、オプションの非球面係数に使用されます。X 方向で非球面係数が必要な場合、座標ブレーク面のペアによってトロイドを回転させ、Z 軸を基準に回転させます。X 方向と Y 方向の両方で異なる非球面が必要な場合は、本書の別の場所で説明する「バイコーニック」面、「多項式」面、「拡張多項式」面を参照してください。
トロイダル面のパラメータ定義
| パラメータ番号 | 定義 |
| 0 | 外挿 |
| 1 | 回転半径 (レンズ ユニット) |
| 2 ~ 8 | α1 ~α7 |
| 13 | 項数 |
| 14 | 正規化半径。この値によって座標が正規化されます。 |
| 15 ~ 245 | ゼルニケ多項式の係数 1 ~ 231 にそれぞれ対応 (レンズ ユニット)。 |
「項数」は、面のサグの計算に使用するゼルニケ多項式の最大項を指定するために使用します。この数は光線追跡の計算速度を上げるために設定するもので、この数を超える項は無視されます。
ゼルニケ多項式は単位円上で直交するので、正規化半径は、係数データが正規化された半径に設定する必要があります。ゼルニケ多項式は正規化半径を越えると急速に発散する傾向があるので、光線がこの半径を越えて面に到達しないように注意する必要があります。光線追跡アルゴリズムは機能するものの、データが不正確になることがあるからです。正規化半径の外に到達する光線のゼルニケ項を無視するために、外挿フラグをゼロに設定できます。
次へ :


