Crosstalk Coefficients
2D Extractor can calculate crosstalk coefficients if you have solved for both the inductance and capacitance matrices.
From the Set View Options window, you can select Crosstalk Coefficients Forward and Crosstalk Coefficients Backward.
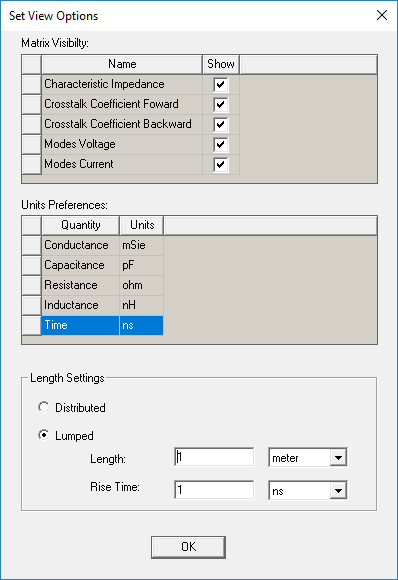
For Crosstalk Coefficients Forward, you can specify:
- Distributed – for crosstalk per unit length/rise time.
- Lumped – for the total crosstalk. This option requires you to enter the Length of the coupled transmission lines and the signal Rise Time. See: Editing the Length Settings.
The following describes these coefficients in greater detail.
Background
Crosstalk coefficients were originally introduced in a classic paper by D. B. Jarvis [IEEE Trans. on Electronic Computers, Oct 1963, p. 476]. Jarvis analyzed the case of two weakly coupled, lossless, transmission lines having the same self-capacitance and inductance values. His paper gave formulas to estimate the crosstalk that would result when one of the lines is driven by a pulse with a finite rise time. Versions 16 and earlier of 2D Extractor implemented Jarvis' formulas in essentially their original form. In version 17 and later, 2D Extractor implements a new set of crosstalk formulas based on an extension of Jarvis' approach to the more general case of transmission lines with different self-inductance and capacitance values. These formulas provide higher accuracy when calculating crosstalk between lines with different LC parameters. The new formulas reduce to Jarvis' original equations when the inductance and capacitance values of the transmission lines are the same.
The formula for the backward crosstalk on line 2 due to a 1-Volt pulse on line 1:

The formula for the forward crosstalk on line 2 due to a 1-Volt pulse on line 1:
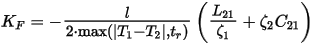
It is important to note that C21 is the off-diagonal term of the per-unit-length Maxwell capacitance matrix. It is typically negative for transmission lines operated in single-ended mode (This might not be true for differential mode). Here l is the length of the lines, T1 and T2 are the time of flight delays, tr is the input signal rise time, and ζ1 and ζ2 are the characteristic impedances.
The derivation of these formulas assumes the driven line is excited by an ideal voltage source at the near end and terminated at the far end in its characteristic impedance. The victim line is assumed to be terminated at both ends in its characteristic impedance. If different terminations or excitations are used, then the crosstalk coefficients may not correctly predict the actual crosstalk. Also note that the formulas assume weak coupling. If coupling is very strong then accuracy may start to degrade. The crosstalk coefficients should only be used as an estimate of the actual crosstalk; they are not a replacement for detailed transient simulation.
Pre-R17 Crosstalk Formulas
If the you set the environment variable ANSYS_R16_CROSSTALK to a non-zero value before invoking the software, then 2D Extractor will revert to using the older version of the crosstalk formulas. These are essentially the original formulas derived by Jarvis.
The pre-R17 formula for backward crosstalk was:
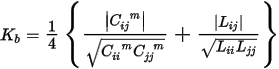
The pre-R17 formula for forward crosstalk coefficient Kf was:
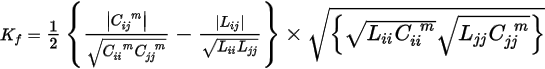
The value of Kf has units of seconds per meter, and is displayed in this form when the Distributed option is selected in the Set View Options dialog box.
The actual forward crosstalk is strongly dependent on the length of the transmission line and the rise time.
To obtain the actual crosstalk the "distributed" Kf value must be multiplied by the line length and divided by the signal rise time. If Lumped crosstalk is selected, then the software performs this multiplication for you and displays a dimensionless number representing the total far end crosstalk.
