Causality

Causality is a property of a system. Simply stated, a causal system initially in a steady state should not show any change in its output until its input signal is changed. Equivalently, a causal system cannot anticipate changes in its input signal and react before those changes occur. One criterion for deciding if a model is physically reasonable is to ask if it is causal.

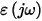
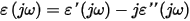
Then the Kramers-Krönig conditions for causality are given by:

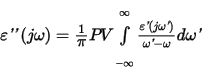
and

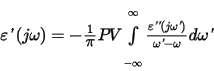
Here PV denotes the Cauchy principal value of the complex integral. The important point to notice about these relations is that the real and imaginary parts of the permittivity are not independent of one another: in fact the real part determines the imaginary part, and vice versa. Therefore, you can not choose the two independently.

The imaginary part of the permittivity is governed by the loss tangent (or, equivalently, the effective conductivity.) This means that the loss tangent and the relative permittivity must be chosen in such a way that the resulting complex permittivity satisfies the above relations. If you are not careful to do this, then the resulting model may not be causal.

When working in the frequency domain, a non-causal model may produce perfectly acceptable results. However, these results are used in a time-domain analysis, they will cause serious problems, such as non-physical transient responses or simulation failures.