Magnetic Field Energy for a Magnetostatic Field Solution

The magnetic energy of a system is given by the following expressions. The expressions represent total values of energy for the volumes taken into account. Note that the integrals have simpler expressions if the material property of the object considered is a linear one. In case of linear material properties magnetic energy and co-energy values are identical (W = W_c).

In linear materials, the energy is

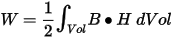
In nonlinear materials, the energy is

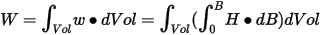
where

H is the magnetic field.
B is the magnetic flux density.

The following figure represents graphically the definitions of both energy and co-energy densities. Note that both are local quantities (i.e. are function of X, Y, Z coordinates of the location in the model) and also depend on the operating point on the applicable B-H curve. Energy is equal to the area above the B-H curve, and coenergy is equal to the shaded blue area below the B-H curve.

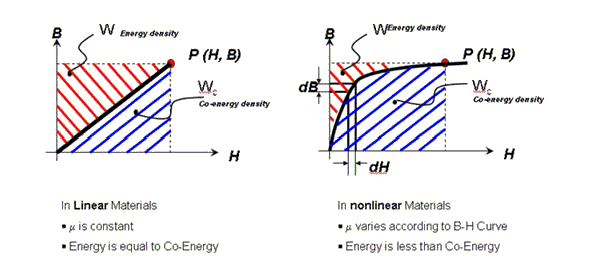
For the sake of brevity, the magnetic flux density in the post processor should be labeled as Magnetic Flux. The total magnetic flux of an object or the whole arrangement can be calculated by integrating over a proper volume in the Field Calculator.

Magnetic Field Energy for a Magnetostatic Field Solution

Related Topics