Magnetic Coenergy for a Magnetostatic Field Solution
The magnetic coenergy of a system is given by the following expressions. The expressions represent total values of co-energy for the volumes taken into account. Note that the integrals have simpler expressions if the material property of the object considered is a linear one. In case of linear material properties magnetic energy and co-energy values are identical (W = Wc).
- In linear materials, the co-energy is
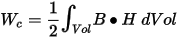
- In nonlinear materials, the coenergy
is
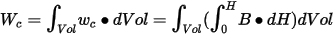
where:
- H is the magnetic field.
- B is the magnetic flux density.
The coenergy is related to the magnetic field energy.
Note: If permanent
magnets are part of the model, as a rule, the magnetic energy reported
by the solver and the postprocessor may be different. This occurs because
the adaptive meshing part of the solution sequence runs a special computation
so that it can avoid situations with a total zero energy of the field
(problems with permanent magnets and no other excitation). To avoid such
situations, the solver uses (and reports) the total energy, which includes
the absolute value of the energy inside the permanent magnets. Because
of this, the energy reported by the solver in these cases is greater
than the energy reported by the postprocessor.
Related Topics
Technical Notes: Magnetic Field Energy
Technical Notes: Magnetic Apparent Energy