A-F Formulation in Maxwell 3D (Transient)

For the Maxwell 3D A-F (A-Phi in the interface) transient solver, solid and stranded conductors, and flux linkage, are defined as described below.

• Solid Conductors

  The Maxwell 3D A-F transient solver is formulated using the magnetic vector potential A and electric scalar potential F. The relations between the potentials and the magnetic field B and electric field E are

  

  

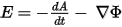
  Using the generalized Ampere’s law, the current continuity equation, and the constitutive relations,

  

  

  

  

  

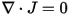
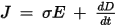
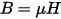
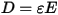
  the time-dependent magnetic equation is expressed as

  

  

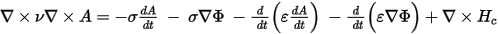
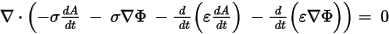
  where

  • H is the magnetic field intensity
  • J is the total current density including source, eddy, and displacement current contributions
  • σ is the conductivity
  • μ is the permeability
  • ε is the permittivity
  • H_c is the coercivity of the permanent magnet
  • n = μ^-1 is the reluctivity.

  Maxwell 3D is used mostly for low-frequency simulations, so the radiation term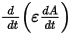in the above equations is ignored in the A-Phi Solver. The first order edge elements for the magnetic vector potential and the second order nodal elements for the electric potential are used. The tree-cotree method is used to ensure the uniqueness of the magnetic vector potential A. The Degrees of Freedom (DOFs) of edge elements on the spanning tree of the finite element mesh are set to zero. The formulation above is used in the entire problem domain except in the stranded conductors.

• Stranded Conductors

  For stranded conductors, the current density is assumed to be constant over the conductor domain, where the eddy and displacement effects are ignored. Therefore, only Ampere’s law is considered in stranded conductors:

  

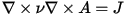
  The solver approximates the constant current density distribution over each conductor for a unit current before the transient solution starts. The approximated unit current density is

  

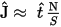
  where

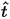  is the current (winding) direction

  I is the total terminal current

  S is the area of the coil terminal into which current is entering

  N is the number of turns

  J is then written as

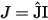
  For winding voltage excitation, the formulation is

  

  

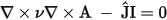
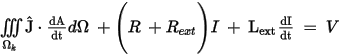
  where R is the DC resistance of the winding, and R_ext and L_ext are, respectively, the external resistance and inductance.

• Flux Linkage

  Flux linkage calculation for windings is relatively easy compared to T-Omega formulation. It is calculated using the equation

  

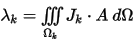
  where J_k is the current density in the winding under 1 A excitation, A is the total magnetic vector potential in the conductor, and Ω_k is the volume of the winding.

Related Topics 

3D Transient Excitations (Sources)