2D Impedance Boundary

Impedance boundaries allow you to simulate the effect of induced currents in a conductor without explicitly computing them. Use this boundary condition for models where:

The skin depth in the conductor is less than two orders of magnitude smaller than the dimensions of the structure. In models like this, the mesh generator may not be able to create a fine enough mesh in the conductor to compute eddy currents.
The magnetic field decays much more rapidly inside the conductor in the direction that’s normal to the surface than it does in directions that are tangential to the surface.
The AC current source is relatively far away from the surface where eddy currents occur, compared to the size of the skin depth.

The conductor itself must be excluded from the solution region. When setting up the model, do one of the following:

For external boundaries, when drawing the model, make the surface along which eddy currents are to be computed an outer surface of the problem region.
For internal boundaries: assign a perfect conductor to the object in the Material Manager, and also exclude the object from the solution by unchecking Solve Inside under the object attributes. The solver does not find solutions inside a perfect conductor.

Then, when defining boundaries, assign an impedance boundary to the individual surfaces of the problem region (for external boundaries) or to the entire object (for internal boundaries). By entering the conductivity, s, and the relative permeability, m_r, of the object, you specify the skin depth of induced eddy currents. The simulator uses this skin depth value when computing the electromagnetic field solution. It assumes that the Magnetic Field falls off exponentially inside the conductor. The ohmic loss due to induced currents can then be computed from the Magnetic Vector Potential along the impedance boundary – on the surface of the object that you are interested in – according to the formula below or by using the quantity EdgeLossDensity in the 2D calculator.

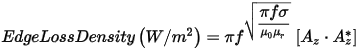
where

A_z = z component of the Magnetic Vector Potential

A_z* = complex conjugate of the z component of the Magnetic Vector Potential

µ₀ = permeability of free space

m_r = relative permeability of the impedance boundary

s = conductivity of the impedance boundary (S/m)

f = frequency (Hz)

You can also use EdgeLossDensity to plot the loss along an edge containing an impedance boundary.

Note: An impedance boundary only approximates the effect of eddy currents acting at a shallow skin depth. It does not directly compute them. In general, the fields modeled using an impedance boundary will closely match the field patterns that would actually occur in the structure. However, at discontinuities in the surface (such as corners), the field patterns may be different.

2D Impedance Boundary

Related Topics