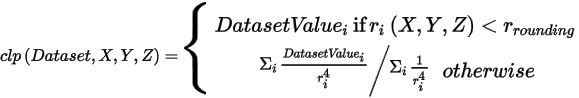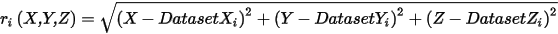Using Intrinsic Functions in Expressions
If units are not specified, all trigonometric functions interpret their arguments as radians. Likewise, inverse trigonometric functions' return values are in given in radians. When the argument to a trigonometric expression is a variable, the units are assumed to be radians. To have values interpreted in degrees, supply the argument with the unit name deg.
The following intrinsic functions may be used to define expressions:
|
Function |
Description |
Syntax |
|
abs |
Absolute value (|x|) |
abs(x) |
|
sin |
Sine |
sin(x) |
|
cos |
Cosine |
cos(x) |
|
tan |
Tangent |
tan(x) |
|
asin |
Arcsine |
asin(x) |
|
acos |
Arccosine |
acos(x) |
|
atan |
Arctangent (in range |
atan(x) |
|
atan2 |
Arctangent (in range |
atan2(y,x) |
|
asinh |
Hyperbolic Arcsine |
asinh(x) |
|
atanh |
Hyperbolic Arctangent |
atanh(x) |
|
sinh |
Hyperbolic Sine |
sinh(x) |
|
cosh |
Hyperbolic Cosine |
cosh(x) |
|
tanh |
Hyperbolic Tangent |
tanh(x) |
|
even |
Returns 1 if integer part of the number is even; returns 0 otherwise. |
even(x) |
|
odd |
Returns 1 if integer part of the number is odd; returns 0 otherwise. |
odd(x) |
|
sgn |
Sign extraction |
sgn(x) |
|
exp |
Exponential (ex) |
exp(x) |
|
pow |
Raise to power (xy) |
pow(x,y) |
|
if |
If |
if(cond_exp,true_exp,false_exp) |
|
pwl |
Piecewise Linear. (pwl can be used with datasets for Design Variables but not for Project variables). |
pwl(dataset_exp,variable) |
|
pwl_periodic |
Piecewise Linear for periodic extrapolation on x. |
pwl_periodic(dataset_exp,variable) |
|
sqrt |
Square Root |
sqrt(x) |
|
ln |
Natural Logarithm (The "log" function has been discontinued. If you use "log(x)" in an expression, the software automatically changes it to "ln(x)".) |
ln(x) |
|
log10 |
Logarithm base 10 |
log10(x) |
|
int |
Truncated integer function |
int(x) |
|
nint |
Nearest integer |
nint(x) |
|
max |
Maximum value of two parameters |
max(x,y) |
|
min |
Minimum value of two parameters |
min(x,y) |
|
mod |
Modulus |
mod(x,y) |
|
rem |
Returns the fractional part of a decimal number such that rem(x) = x-int(x) |
rem(x) |
| clp |
Implements smooth interpolation employing weighted impact of all points of the dataset (not just the closest one). See formula below. Note: If used with a large 3D dataset, clp function will degrade. |
clp(datasetName, X,Y,Z) |
clp Formula