Adaptive Single Objective Optimization
Adaptive Single-Objective (ASO) is a mathematical optimization method that combines an OSF (Optimal Space-Filling) DOE, a Kriging response surface, and MISQP. It is a gradient-based algorithm based on a response surface, which provides a refined, global, optimized result.
ASO supports a single objective and multiple constraints. It is available for continuous parameters, including those with manufacturable values. It does not support the use of parameter relationships in the optimization domain and is available only for a Direct Optimization system.
Like MISQP, ASO solves constrained nonlinear programming problems of the form:
Minimize:
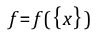
Subject to:
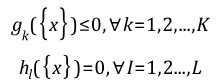
Where:
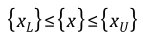
ASO Workflow
The workflow of ASO follows:
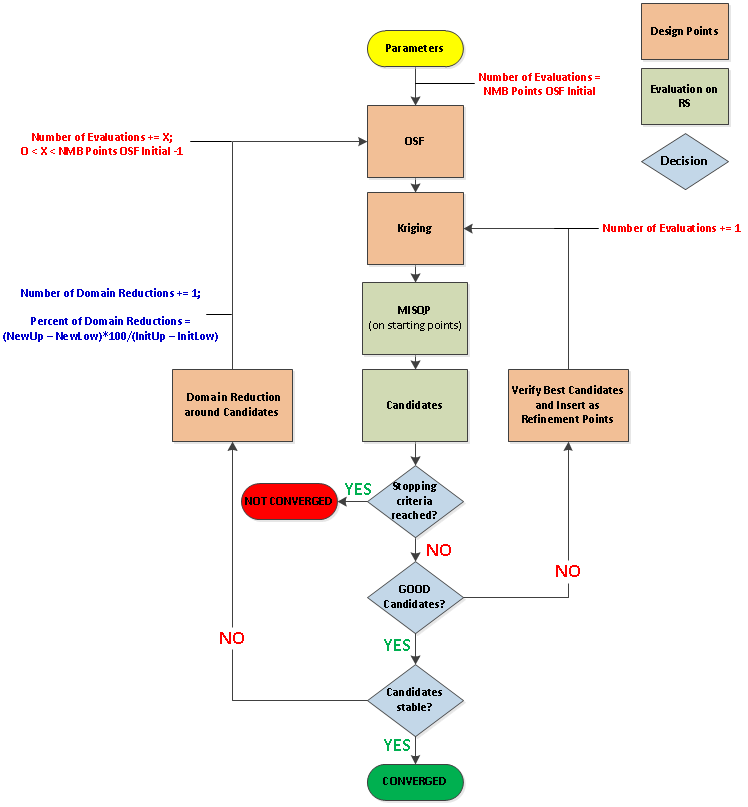
AMO Steps
- OSF Sampling
OSF (Optimal Space-Filling Design) is used for the Kriging construction. In the original OSF, the number of samples equals the number of divisions per axis and there is one sample in each division.
When a new OSF is generated after a domain reduction, the reduced OSF has the same number of divisions as the original and keeps the existing design points within the new bounds. New design points are added until there is a point in each division of the reduced domain.
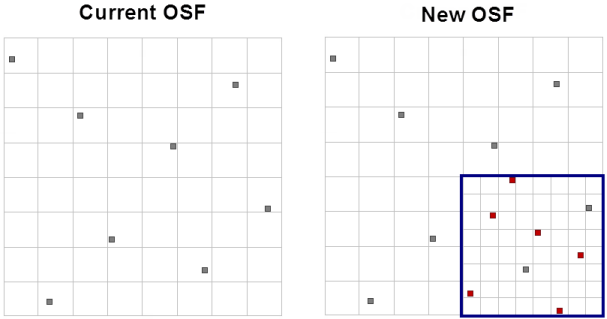
In the following example, the original domain has eight divisions per axis and contains eight design points. The reduced domain also has eight divisions per axis and includes two of the original design points. To have a design point in each division, six new design points need to be added.
- Kirging Generation
A response surface is created for each output, based on the current OSF and consequently on the current domain bounds.
A Kriging response surface is created for each output, based on the first population and then improved during simulation with the addition of new design points.
For more information on Kriging algorithms, see Kriging Algorithms.
- MISQP
MISQP is run on the current Kriging response surface to find potential candidates. A few MISQP processes are run at the same time, beginning with different starting points, and consequently, giving different candidates.
- Candidate Point Validation
All the obtained candidates are either validated or not, based on the Kriging error predictor. The candidate point is checked to see if further refinement of the Kriging surface changes the selection of this point. A candidate is considered as acceptable if there aren't any points, according to this error prediction, that call it into question. If the quality of the candidate is not called into question, the domain bounds are reduced. Otherwise, the candidate is calculated as a verification point.
- Refinement Point Creation (If the selection is not to be changed)
- Domain Reduction(If the selection is to be changed)
When candidates are validated, new domain bounds must be calculated. If all of the candidates are in the same zone, the bounds are reduced, centered on the candidates. Otherwise, the bounds are reduced as an inclusive box of all candidates. At each domain reduction, a new OSF is generated (conserving design points between the new bounds) and a new Kriging response surface is generated based on this new OSF.
When a new verification point is calculated, it is inserted in the current Kriging response surface as a refinement point and the MISQP process is restarted.
- Convergence and Stop Criteria
The optimization is considered to be converged when the candidates found are stable. This occurs when all of the MISQP processes run on the response surface converge to the same verified candidate point. However, there are four stop criteria that can stop the algorithm: Maximum Number of Evaluations, Maximum Number of Domain Reductions, Percentage of Domain Reductions, and Convergence Tolerance.
