The study of the equations of motion for a particle is fundamental in understanding the dynamics of single and multiple-body systems. These equations, derived from Newton's second law, form the basis for analyzing the forces and movements acting on a particle in an XY plane. This section provides a comprehensive overview and extension of the foundational equations governing a particle's motion, employing both vector and variational forms for a holistic understanding.
At the core of particle dynamics is Newton's second law, which states that the force acting on a particle is equal to the mass of the particle multiplied by its acceleration. For a particle moving in a plane, this can be expressed in the Cartesian coordinate system as:
 | (2–113) |
 | (2–114) |
where:
 = mass of the particle |
 and  = accelerations of the particle in the x and y directions,
respectively |
 and  = components of the force acting on the particle in the x
and y directions, respectively |
This form illustrates that the net force minus the product of mass and acceleration equals zero, which is consistent with the principle of equilibrium in dynamics.
The variational form of the equations introduces the concept of virtual work (δW) and virtual displacement (δq), offering a powerful method for analyzing systems under constraints. It is given by:
 | (2–115) |
The same equations of motion can be expressed in the variational form as:
 | (2–116) |
where:
| δW = virtual work |
| δq = virtual displacement (this is arbitrary) |
This equation is derived from the principle of virtual work, which posits that for a system in equilibrium, the virtual work done by the forces during an arbitrary virtual displacement is zero.
The variational form of the equations of motion for a body without constraints is:
 | (2–117) |
The variational form of the equations of motion for multiple bodies without constraints is given by:
 | (2–118) |
where:
 = virtual displacement of the
ith generalized coordinate |
 = diagonal mass matrix for the
ith body |
 = the acceleration of the ith
body |
 = the generalized force acting on the
ith body |
 = number of bodies |
Since δq_i is arbitrary, so 
must be zero. Therefore, the equation is organized as
follows:
 | (2–119) |
For equations of motion for systems with constraints, see Lagrange Multiplier Method.
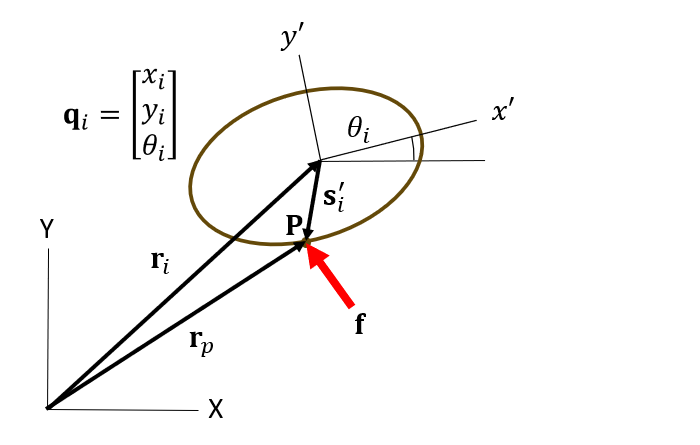
When an any force is applied to a body within a multibody system, it is not directly used in its raw form in the equations of motion. Instead, it undergoes a transformation into what is known as a generalized force. A generalized force is defined as the force corresponding to a generalized coordinate that contributes to the work done on a system. It's a pivotal concept in the multibody dynamics, translating the physical forces and moments acting on a system into a form directly applicable within the system's equations of motion.
When a force f acts at a location on the body other than the body reference frame, and the generalized coordinates are xi, yi and θi, the principle of virtual work dictates that the virtual work is:
 | (2–120) |
 | (2–121) |
 | (2–122) |
Thus, generalized force Q is:
 | (2–123) |
Finally, equations of motion of the system are:
 | (2–124) |
where:
 = virtual work |
 = position of the body reference frame.  |
 = position of the point P,  |
 = virtual displacement from the generalized
coordinates |
 = virtual displacement from the point p |
 = generalized force |
 = mass matrix of the system.  |
 = mass of the system |
 = moment of the inertia of the body |