This is a relatively simple strength model designed to represent the crush characteristics of foam materials under impact loading conditions (non-cyclic loading).
The model principal stress vs volumetric strain behavior is shown below.
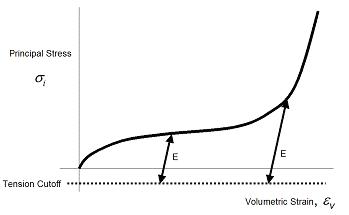
The strength model must be used with isotropic elasticity and the following incremental elastic update of pressure and stress deviators is used.
In tension, the model additionally includes the possibility to apply a tension cut-off to the maximum allowable principal tensile stress. If the tensile stress exceeds this value, it is maintained at this value. The model cannot currently be used with other failure properties.
Note: This property must be used in combination with isotropic elasticity.
The property can only be applied to solid bodies.
Note that the plastic strain variable is used to store the inelastic volumetric strain for this porosity model.
Table 11.16: Input Data
| Name | Symbol | Units | Notes |
|---|---|---|---|
| Maximum Principal Stress vs Volumetric Strain | Stress and strain | Tabular data | |
| Maximum Tensile Stress | Stress |
Custom results variables available for this model:
| Name | Description | Solids | Shells | Beams |
|---|---|---|---|---|
| EFF_PL_STN | Effective Plastic Strain | Yes | No | No |
| PRESSURE | Pressure | Yes | No | No |
| DENSITY | Density | Yes | No | No |
Porous Materials
Porous materials are extremely effective in attenuating shocks and mitigating impact pressures. The material compacts to its solid density at relatively low stress levels but, because the volume change is relatively large, a large amount of energy is irreversibly absorbed thereby attenuating shocks by lengthening the wave in time and reducing it in amplitude as more material is compacted.
Cellular porous materials contain a population of microscopic cells separated by cell walls. When stressed the initial elastic compression is assumed to be due to elastic buckling of the cell walls and the plastic flow to be due to plastic deformation of these cell walls. Materials with low initial porosity has fewer cells and thicker cell walls so that the stress required to cause buckling and subsequent deformation of the cell walls will be greater.
Once some plastic flow has taken place, even if the fully compacted density hasn't been reached, unloading to zero stress and reloading to the elastic limit will be elastic. This phenomenological behavior is illustrated in the following figure.


