When sliding mesh technique is used, two limitations of the mixing module forbid the use of the computed flow field to perform tracking of material points. Firstly, in the case of transient simulations, the mesh can / will change with time (position of the nodes). Secondly, the mesh is non-conformal. As the tracking of material points does not allow such cases, we propose the following procedure:
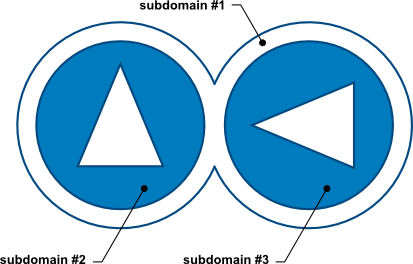
In your mesher application, define a mesh constituted of different subdomains for the flow domain: one subdomain is fixed, while the other(s) is (are) rotating. In the figure below, the flow domain is composed of disconnected subdomains 1 to 3. The subdomain #1 is fixed, while subdomain #2 is rotating with the left cam and subdomain #3 is rotating with the right cam. The internal part of the cams are not be meshed.
In Polydata, during the definition of the flow task, we use the sliding mesh technique; we define motion of the rotating subdomains. Connected boundary conditions are needed between tangential boundaries of fixed and rotating subdomains. Moreover, we ask for the output of CSV results files.
In Polyflow, we evaluate the transient flow, using sliding mesh technique; at each time step, a CSV file is generated that contains the current flow field.
In your mesher application, define a new mesh, where the flow domain is conform, and with new subdomains overlapping the flow domain and corresponding to the moving parts (as if we had to define subdomains for the mesh superposition technique). The position of the moving parts must correspond to the initial position of the moving parts used for the simulation of the flow field!
In Polydata, we perform a conversion of the csv files into new Polyflow results files onto this new mesh (the mesh of the flow domain will remain constant in time); at the end of this step, we have a set of res files (1 res file per time step) compatible with the new mesh.
In Polydata, we define a mixing task, based on the new mesh and the new results files.
In Polyflow, we compute the trajectories of a set of material points.
In Polystat, we perform a statistical analysis on these trajectories.