Returns a variable of the same type and dimensions as the first argument x, filled with random values. The second argument dt specifies the distribution type and p must be a vector with the distribution parameters. In detail:
For type UNIFORM argument p must be a two dimensional vector [a, b] and the function returns values uniformly distributed in the range [a..b).
The type NORMAL expects p as a two dimensional vector [a, b] and produces random numbers distributed with probability density function
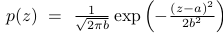
The type LOGNORMAL expects p as a two dimensional vector [a, b] and produces random numbers distributed with probability density function
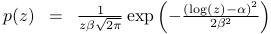
for x > 0, where

and
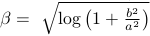
The type TRIANGLE expects p as a three dimensional vector [a, b, c] and returns values in the range [a,c]. The function then uses triangle distribution, where b is the most probable value.
For type EXPONENTIAL p must be a one dimensional vector [a] and the function returns random numbers distributed with probability density function
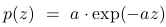
The type CAUCHY expects p as a two dimensional vector [a, b] and produces random numbers distributed with probability density function
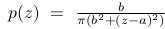
Syntax
rand(x,dt,p)
Types
| Variable Name | Value Type | Variable Type | ||
|---|---|---|---|---|
| Arguments: | x | real, complex | scalar, vector, matrix, signal, xy-data | |
| dt | type | [UNIFORM, NORMAL, LOGNORMAL, TRIANGLE, EXPONENTIAL, CAUCHY] | ||
| p | real | scalar, vector | ||
| Result: | v | real, complex | scalar, vector, matrix, signal, xy-data | |
Calculator Input
Use the button to complete the operation.
Example
| ID | Description | Type | Value | Expression | |
|---|---|---|---|---|---|
| x | Argument | REAL VECTOR |
| [1,1,1] | |
| p | Argument | REAL VECTOR |
| [2,4] | |
| v | Result | REAL VECTOR |
| rand(x,UNIFORM,p) | |


