VM-LSDYNA-SOLVE-008

VM-LSDYNA-SOLVE-008
Steady State Thermal Analysis of a Beam

Overview

Reference:	Kreith, F. (1959). Principles of Heat Transfer (2nd ed.). International Textbook Co.
Analysis Type(s):	Steady State Thermal
Element Type(s):	Beam
Input Files:	Link to Input Files Download Page

Test Case

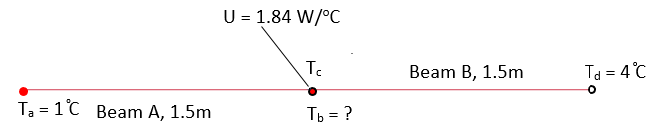
Isotropic steel beams A and B are separated by an area with thermal conductance U = 1.84 W/°C. Beams A and B are of equal length L = 1.5 m, thermal conductivity k = 46 W/(m°C), and cross-sectional area A = 0.04 m². The far end of beam A has a temperature of 1°C. The opposite end of beam B has a temperature of 4°C. Find the steady state temperature T_b on beam A.

Figure 34: Problem Sketch

Material Properties	Geometric Properties	Loading
k = 46 W/(m°C)	L_ab= 1.5 m	T_a= 1°C
U = 1.84 W/°C	L_cd= 1.5 m	T_d = 4°C

Analysis Assumptions and Modeling Notes

LS-DYNA Thermal Solver 3 is used. The steel beams are modeled using ELFORM 1. Conduction between beams is constrained using a zero-length discrete beam with ELFORM 6. Temperature boundary conditions are applied using keyword *BOUNDARY_TEMPERATURE.

Figure 35: Heat Flow Model

At steady state, the rate of heat dissipation Q

And the thermal resistances R_ab, R_cd, and R_bc can be expressed as:

From the above equations, the analytical solution of T_b is obtained as 2.125°C.

Figure 36: Fringe plot of temperature °C in the model

Results Comparison

	Target	LS-DYNA	Error (%)
Temperature at T_b	2.125°C	2.122°C	0.14%