VM-LSDYNA-WB-005
VM-LSDYNA-WB-005
Pinned Bar Under Gravity Loading
Overview
| Reference: | W. G. McLean, E. W. Nelson, & C. L. Best. (1978). Schaum's Outline of Theory and Problems of Engineering Mechanics, Statics and Dynamics. New York: McGraw-Hill Book Co. 336. |
| Analysis Type(s): | Explicit Dynamics with Workbench LS-DYNA |
| Element Type(s): | Explicit 3-D Beam Elements |
| Input Files: | Link to Input Files Download Page |
Test Case
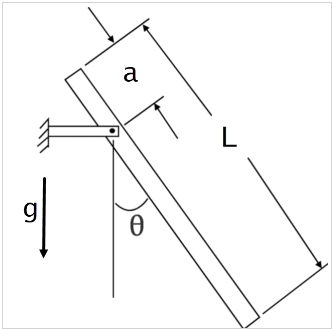
A homogeneous bar with total length L is pinned as shown below. The distance from the end of the bar to the pin is represented by the distance a. The bar is subjected to gravity loading and its initial position is θ = 30° from the vertical. The rotational speed when it passes through θ = 0° is calculated and compared to an analytical expression.
| Material Properties | Geometric Properties | Loading | |||
|---|---|---|---|---|---|
|
Density = 1.0 kg/m3 Modulus of Elasticity =
Poisson's Ratio = 0.30 |
Constant square cross-section of 0.1 x 0.1 m2 Total Length:
|
The acceleration due to gravity is 9.8 m/s2 in the y-direction. One node is constrained in UX, UY, and UZ. All other nodes are constrained only in UZ. At y = 0, UY = 0 |
Analysis Assumptions and Modeling Notes
Twenty-eight beam elements were used to model the bar.
The material properties are arbitrary. As noted in the reference (McLean et al., 1978), assuming the bar is released at θ = 30°, the magnitude of the bar's angular velocity when θ = 0° can be written as:
Given the geometry, when the bar passes through θ = 0°, ω = vx / 0.75, where vx is the translational velocity in the global Cartesian x-direction of the end of the bar.
Directional velocity in x-direction at θ = 0° (t = 0.4 s) is measured at the end of the bar.
| vx = 1.552 m/s |
| ω = vx / 0.75 = 2.07 rad/s |