Basic Infill Shapes

Extrusions


Square Extruded square grid.
Triangle Extruded triangle grid.
Hex Extruded hexagonal grid.
3D Hex 3D hexagonal grid similar to honeycomb structures. Cross-sections alternate between hexagons and square.

Lattices

Select a Lattice structure and Lattice trimming option.


Lattice Three dimensional lattice infill pattern
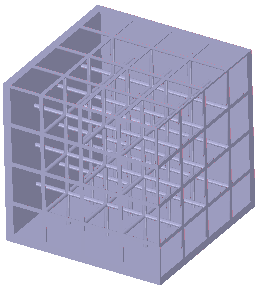
Regular Cube Lattice Simple cube lattice infill pattern
Cube Lattice with Center Supports Cube lattice with supports from all corners of the cube intersecting at the center of the cube
Cube Lattice with Side Cross Supports Cube lattice with cross supports between edges on each face of the enclosing cube
Cube Lattice with Side Diagonal Supports Cube lattice with diagonal supports between vertices on each face of the enclosing cube
Cube Lattice with Bottom Center Cube lattice with supports that meet at the bottom face center of the enclosing cube
Cube Lattice with Bottom Center Without Vertical Supports Cube lattice with supports that meet at the bottom face center of the enclosing cube but without vertical supports
Double Pyramid Lattice Double pyramid lattice with lateral supports
Double Pyramid Lattice with Cross Double pyramid lattice with internal cross supports
Diamond Lattice Double pyramid without the lateral supports
Double Pyramid Lattice and Face Diagonals Double pyramid in the center of the lattice with diagonals on faces of the enclosing cube
Octahedral-1
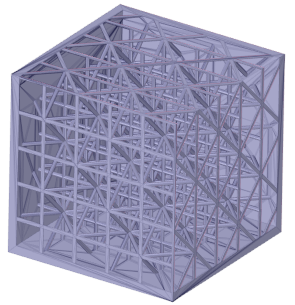
Octahedral-2
Tetrahedral Faceted Lattice Boundary conforming lattice structure, where the lattice elements follow the edges of tetrahedra.
Triangle Surface Faceted Lattice Uniform surface lattice, smoothly connected at the vertices with triangular holes.
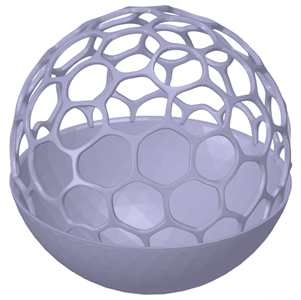
Hexagon Surface Faceted Lattice Smoothed Voronoi dual to the triangular surface mesh. Holes are on average hexagonal.

Select a lattice trim option:


None: No explicit trimming is done. The internal lattice structure is trimmed by the original part, which may leave dangly lattice pieces that are not connected to other lattice pieces
Remove partial segments: trims the dangling pieces back so that every lattice has at least two lattice edges ending in it.
Boundary conforming: builds a Triangular Lattice between the surface of the geometry shell and the interal lattice structure.

Note:

The Boundary conforming and Remove partial segments options are not available for the following lattice types, since they are already boundary conforming by design.
- Tetrahedral Faceted Lattice
- Triangle Surface Faceted Lattice
- Hexagon Surface Faceted Lattice
Lattice trimming is not available for the three dimensional infill pattern "Lattice".

Minimal Surfaces


Gyroid Belongs to Triply Periodic Minimal Surfaces.
Schwarz P Two intertwined congruent labyrinths, each with the shape of an inflated tubular version of the simple cubic lattice.
Schwarz D Two intertwined congruent labyrinths, each having the shape of an inflated tubular version of the diamond bond structure.
Neovius A triply periodic minimal surface, dividing space into two infinite non-equivalent labyrinths.
Lidinoid A triply periodic minimal surface similar to a gyroid.

You can choose to add a smooth transition from the minimal surface infills to the boundary of the original part. Select Boundary transition and specify an appropriate value for Radius to add a smooth blend to the boundary.