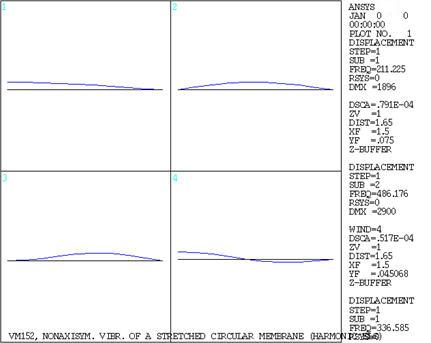
VM152
VM152
2D Nonaxisymmetric Vibration of a Stretched Membrane
Test Case
A circular membrane under a uniform tension S is allowed to
vibrate freely. The edge of the membrane is simply supported. Determine
the natural frequencies fi,j for the first
mode of vibration (j = 1 = no. of nodal circles, including the boundary)
for the first three harmonic (i = 0,1,2 = no. of harmonic indices).
Also determine the next highest axisymmetric frequency f0,2. See VM153 for a 3D solution of this problem.
Analysis Assumptions and Modeling Notes
A total of 9 elements is selected for meshing. The prestress
is induced by cooling the membrane. The necessary temperature difference, ΔT,
is calculated from S = -E αt(ΔT). Modal analysis is solved using Block-Lanczos eigensolver.
Results Comparison
Window 1 - f0,1; Window 2 - f1,1; Window 3 - f2,1; Window
4 - f0,2;