赛德尔系数(Seidel Coefficients)

显示(未转换的、垂轴和轴向的)赛德尔以及波前像差系数。
波长(Wavelength) 计算中使用的波长编号。
详述
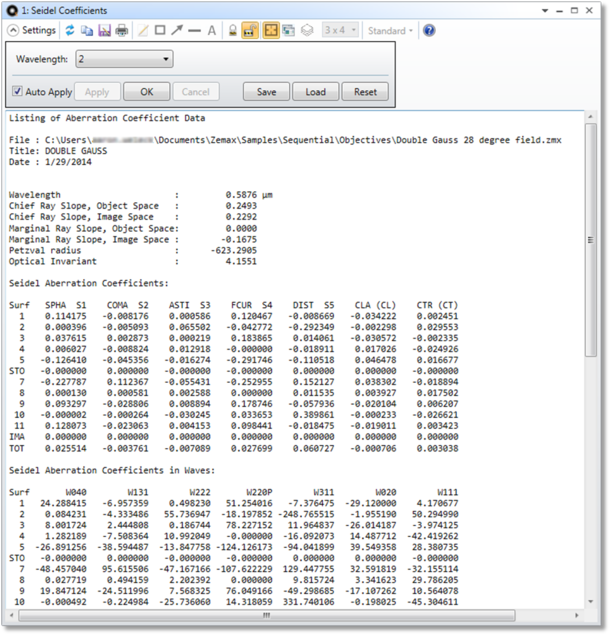
OpticStudio将计算未转换的赛德尔系数、垂轴、轴向和一些波前系数。赛德尔系数以及整个系统的赛德尔总和将按表面顺序列出。列出的系数包括球差(SPHA, S1)、彗差(COMA, S2)、像散(ASTI, S3)、场曲(FCUR, S4)、畸变(DIST, S5)、轴向色差(CLA, CL)和垂轴色差(CTR, CT)的系数。单位通常与系统选项中的镜头单位相同,但以波数为单位测量的系数除外。
这些计算仅对完全由轴对称球面、圆锥面、二阶或第四阶非球面构成的系统有效,且计算准确。这些系数的计算是通过近轴光线得到的,而对于包含坐标断点面、光栅面、近轴面或其它非径向对称表面的系统,近轴光线不能充分描述整个系统。具体而言,这些计算支持的表面类型有标准面、偶次非球面、奇次非球面、扩展非球面和扩展奇次非球面。
每个表面和系统整体的垂轴像差系数被一一列出。包括垂轴球差(TSPH)、垂轴弧矢慧差(TSCO)、垂轴子午彗差(TTCO)、垂轴像散(TAST)、垂轴Petzval场曲(TPFC)、垂轴弧矢场曲(TSFC)、垂轴子午场曲(TTFC)、垂轴畸变(TDIS)、垂轴轴向色差(TAXC)和垂轴倍率色差(TLAC)的系数。垂轴像差是以系统镜头单位为单位。在光线几乎准直的光学空间中,垂轴像差系数可以很大,这些系数在这些光学空间中几乎没有意义。
Petzval半径是Petzval总和的倒数,定义如下:
其中ni-1和ni分别是表面i之前和表面i之后的折射率。Ri是表面i的曲率半径。nm是像面的折射率。m是像面的表面编号。
在计算Petzval半径时,会将物空间和像空间的折射率的绝对值都考虑进去。此计算中忽略物面和像面半径。
可计算以下轴向像差系数,包括轴向球差(LSPH)、轴向弧矢彗差(LSCO)、轴向子午彗差(LTCO)、轴向像散(LAST)、轴向Petzval场曲(LPFC)、轴向弧矢场曲(LSFC)、轴向子午场曲(LTFC)、轴向畸变(LDIS)、沿轴轴向色差(LAXC)和轴向倍率色差(LLAC)。轴向像差是以系统镜头单位为单位。在光线几乎准直的光学空间中,轴向像差系数可以很大,这些系数在这些光学空间中几乎没有意义。
波前系数包括球差(W040)、慧差(W131)、像散(W222)、Petzval场曲(W220P)、畸变(W311)、轴向色差离焦项(W020)、垂轴色差倾斜项(W111)、弧矢场曲(W220S)、中间场曲(W220M)和子午场曲(W220T)的系数。所有波前系数均以出瞳边缘的波长单位为单位。各种像差系数根据下表相互关联。n’和 u’值分别是系统最后一面的折射率和近轴边缘光线角。有关赛德尔像差系数的含义和公式推导的详述,请参阅Welford 的《Aberrations of Optical Systems》、Smith的《Modern Lens Design》或O' Shea的《Elements of Modern Optical Design》。有关参考书目的列表,请参阅"镜头设计参考(References on Lens Design)"。
| 名称 | 赛德尔 | 波 | 描述 | 横向 | 轴向 |
|
球差 |
|
|
球差 |
|
|
|
彗差 |
|
|
弧矢 |
|
|
| 子午 |
|
|
|||
| 像散 |
|
|
从子午到弧矢焦点 |
|
|
|
场曲 |
|
|
高斯到Petzval |
|
|
|
|
|
高斯到弧矢 |
|
|
|
|
|
|
高斯到中间 |
|
|
|
|
|
|
高斯到子午 |
|
|
|
|
畸变 |
|
|
畸变 |
|
|
| 轴向色差 |
|
|
已定义的极端波长之间测量的色差(参考所选波长)。 |
|
|
| 垂轴色差 |
|
|
|
|
赛德尔系数很容易与波前像差相关:
S1 = 8 W040
S2 = 2 W131
S3 = 2 W222
S4 = 4 W220 - 2 W222
S5 = 2 W311
下一部分:


