FFT PSF

使用快速傅里叶变换(FFT)算法计算衍射点扩散函数 (PSF)。
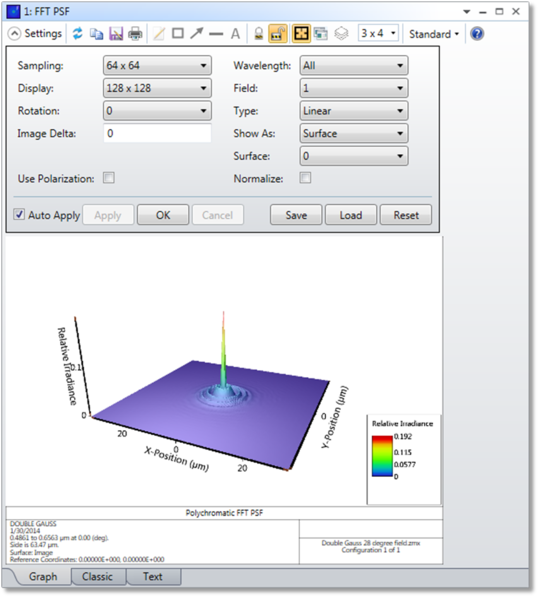
采样(Sampling) 用于进行光瞳采样的光线网格的尺寸。采样可以是32x32、64x64,等等。虽然更高的采样率会产生更准确的数据,但计算时间会增加。
显示(Display) 表示生成绘图显示时将绘制哪部分计算数据。显示网格可以是从32 x 32到两倍采样网格尺寸的 任意大小。显示大小越小,显示的数据越少,但放大率越高,可见性越好。此控件不会对文本显示产生任何影响。
旋转(Rotation) 旋转指定了为便于查看的表面图的旋转方式;可以是0、90、180度,也可以是270度。
波长(Wavelength) 计算中将使用的波长编号。
视场(Field) 计算中使用的视场编号。
类型(Type) 选择"线性"(强度)、"对数"(强度)、"相位"、(有正负符号振幅的)"实部"或(有正负符号振幅的)"虚部"。
显示为(Show As) 选择表面图、等高线图、灰阶或伪彩色图作为显示选项。
使用偏振(Use Polarization) 如果选中,则将考虑偏振。有关如何定义偏振态和通过分析功能如何使用偏振的信息,请参阅"偏振(系统选项)(Polarization (System Explorer))"。
像面采样间距(Image Delta) 像方各点之间的delta距离(以微米为单位)。如果为零,则使用默认间隔。如果为负值,则像面采样间距设置为允许的最大值,且使用全采样网格。查看"详述",了解详情。
归一化(Normalize) 如果选中,会把峰值强度归一化为统一。如果未选中,峰值强度将归一化为无像差PSF(斯特列尔比(Strehl ratio))的峰值。
表面(Surface) 选择要评估的点扩散函数所位于的表面。这对于评估中间图像非常实用。请参见"评估中间面上的结果(Evaluating results at intermediate surfaces)"。
详述(Discussion)
使用FFT算法计算点扩散函数速度很快,但其中包含了一些假设,这些假设并非始终成立。惠更斯算法虽然计算速度较慢,但更为通用,包含的假设较少,参阅"惠更斯PSF(Huygens PSF)"中提供的详细说明。
FFT PSF计算所使用的假设
FFT PSF可计算视场中单个点光源在光学系统中形成的衍射图像的强度。在与参考波长入射主光线垂直且将主光线作为中心的假想平面上计算的强度。多波长计算中使用主波长作为参考波长,或在单波长计算中使 用单波长作为参考波长。由于假想平面与主光线垂直,且不是像面,因此在主光线入射角度不为零时计算的FFT PSF结果过于乐观(会得到更小的PSF);这通常是包含倾斜像面的系统、广角系统、异常出瞳系统或非远心系统会出现的情形。
FFT算法做出的其它主要假设有,像面位于光束的远场。这意味着仅当像面很接近所有光线的几何焦点时,计算的PSF才准确;或者换言之,横向光线像差不能过大。虽然没有硬性限制,但如果横向像差超过几百个波长,则计算可能不准确。注意:即使波前差很小的系统也可以有很大的横向光线像差;例如,仅沿一个方向会聚光线的柱面透镜。在此情况下,非聚焦方向的横向像差与光束直径近似。在这些情况下,惠更斯PSF方法也可以提供更准确的结果。
对于大多数透镜,相比前面提到的假设来说不太重要的假设是应用了标量衍射理论。不考虑光线的矢量性。这一点在接近或小于F/1.5(在空气中)的快速系统中很重要。标量衍射理论在F/#值很小时预测的结果(较小PSF)过于乐观。
如果系统的主光线与像面几乎垂直(角度可能小于20度),出瞳像差是可以忽略的,且横向光线像差合理,则FFT PSF是准确的,并且速度通常比惠更斯PSF方法快得多。
如果存在疑虑,应采用这两种PSF方法进行比较。深入理解用户环节的这些假设和计算方法,对于辨别可能损坏准确性的情况非常重要。
关于FFT方法和采样问题的详述
FFT PSF算法利用了衍射PSF与光学系统出瞳处的波前复振幅的傅里叶变换相关这一事实。先在出瞳处对光线网格计算振幅和相位,再进行FFT,然后计算衍射图像强度。
在光瞳上的采样网格尺寸与衍射图像上的采样周期两者间选择一个折衷方案。例如,要减少衍射图像的采样周期,必须增加光瞳的采样周期。为此,"拉伸"光瞳采样网格,以使其填满光瞳。此过程意味着光瞳中的点实际将减少。
随着采样网格尺寸增加,OpticStudio将调整光瞳网格以增加光瞳上的点数,同时使衍射图像的采样更密集。网格尺寸每次翻倍后,光瞳采样周期(光瞳中两点之间的距离)各维度将按2的平方根减少,像面采样周期各维度也将按2的平方根减少,衍射图像网格宽度将以2的平方根为因子增加(因为每个维度中有两倍的点数)。所有比率都是近似比,并且对大网格是接近正确的。
尺寸拉伸参考于32 x 32网格。将32 x 32网格中的点放在光瞳上,并对光瞳中的点进行追迹。对于该网格尺寸,计算衍射像面两点之间默认距离的公式是
其中F是工作F/#(与像空间F/#不同),是最短定义波长,而n是网格中的点数。因子-2是因为光瞳不在网格中心(因为n是偶数),而是偏移了n/2 + 1。分母中的2n是由于后面描述的零填充。
对于大于32 x 32的网格,网格在光瞳空间中的默认拉伸系数为采样密度每次会翻倍。像空间采样的通用公式是
像面数据网格的总宽度是
由于拉伸光瞳网格会减少光瞳中的采样点数,因此有效网格尺寸(表示实际追迹光线的网格尺寸)比采样网格小。有效网格尺寸将随采样增加而增加,但不如采样增加得快。下表总结了各种采样密度值的近似有效网格尺寸。
点扩散函数计算的默认有效网格尺寸
| 采样网格尺寸 | 近似有效光瞳采样 |
| 32 x 32 | 32 x 32 |
| 64 x 64 | 45 x 45 |
| 128 x 128 | 64 x 64 |
| 256 x 256 | 90 x 90 |
| 512 x 512 | 128 x 128 |
| 1024 x 1024 | 181 x 181 |
| 2048 x 2048 | 256 x 256 |
| 4096 x 4096 | 362 x 362 |
| 8192 x 8192 | 512 x 512 |
采样也是波长的函数。上文详述仅对计算所使用的最短波长有效。如果计算是多波长计算,则会调整较长波长,以使用较小的有效网格。所使用的比例因子是波长比。在为宽波长段系统选择采样网格时,应考虑这个问题。对于多波长计算,短波长得到数据比长波长的数据更准确。对于FFT PSF相位、实部和虚部数据类型,多波长平均值没有实际意义,并且如果用户选择所有波长,OpticStudio会将波长选项设置为主波长。
如果需要不同的采样距离,可以手动选择像面采样间距Δ。如果像面采样间距为零,则OpticStudio会使用上述间隔和采样网格。如果像面采样间距大于零,则OpticStudio会调整光瞳采样以生成所需像面采样间距大小。实际拉伸量取决于网格尺寸、像面采样间距、定义的波长、各视场和波长的F/#值以及出瞳的纵横比。如果像面采样间距设置得过小,则无法留下足够的光瞳采样点;如果像面采样间距过大,则光瞳网格无法遍布整个出瞳宽度。OpticStudio已控制这两种情况,在出现这些情况时,系统会发出错误消息。如果像面采样间距小于零,则OpticStudio根本不会拉伸光瞳。这样可最大程度地扩大像坐标中的PSF范围,并使用光瞳中全网格的光线,但采样的空间分辨率不会增加,因为像面采样间距会因采样增加几乎保持不变。
在指定采样后,OpticStudio会在所谓的"零填充"过程中使阵列尺寸翻倍。对于32 x 32采样,这意味着OpticStudio会使用64 x 64网格的中心部分。因此,衍射点扩散函数将分布在64 x 64大小的网格上。像空间中的采样始终是光瞳采样的两倍。零填充可减少混叠现象。
FFT算法的本质是在光瞳空间坐标中完成计算。因此,旋转像面不会影响计算的PSF的方向。PSF的X和Y方向与入瞳中光线的X和Y方向对应,但与像的X和Y空间方向不是始终相同的。要在像空间坐标中计算PSF,请参阅"惠更斯PSF"
下一部分:


