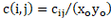切比雪夫多项式(Chebyshev Polynomial)

切比雪夫多项式曲面是一个由基本曲率半径和切比雪夫多项式序列描述的自由曲面。首先给出第一类一维切比雪夫多项式：

作为参考，前十个切比雪夫多项式系数如下：

T₀ (x) = 1

T₁ (x) = x

T₂ (x) = 2x² – 1

T₃ (x) = 4x³ - 3x

T₄ (x) = 8x⁴ - 8x² + 1

T₅ (x) = 16x⁵- 20x³ + 5x

T₆ (x) = 32x⁶ - 48x⁴ + 18x² – 1

T₇ (x) = 64x⁷ - 112x⁵ + 56x³ - 7x

T₈ (x) = 128x⁸ - 256x⁶ + 160x⁴ - 32x² + 1

T₉ (x) = 256x⁹ - 576x⁷ + 432x⁵ - 120x³ + 9x

T₁₀ (x) = 512x¹⁰ - 1280x⁸ + 1120x⁶ - 400x⁴ + 50x² - 1

通过使用系统的t_ij（x,y）基准形式，实现一个二维切比雪夫(Chebyshev)多项式的过渡：

在OpticStudio，x和y的最大阶数设置为14。任何函数都可以插值为切比雪夫多项式项的有限和：

在单位区间上定义了二维切比雪夫多项式的参数。为了使插值对任意区间有效，我们使用归一化的与作为多项式的参数。

那么"矢高"或切比雪夫多项式曲面z坐标给出如下：

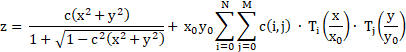
其中，c是表面的顶点曲率，与是归一化长度，而是归一化多项式系数。

切比雪夫曲面在归一化半径X0和Y0之外未进行定义。在归一化半径之外入射到切比雪夫曲面的光线无法被追迹，并且会在切比雪夫曲面上形成渐晕。

切比雪夫多项式曲面的参数定义

参数#	名称	定义
1	X最大阶数	在横坐标最大多项式的阶数（整数，最多14）
2	Y最大阶数	在纵坐标最大多项式的阶数（整数，最多14）
3	标准化X长度	归一化长度（正数，默认为1）
4	标准化Y长度	归一化长度（正数，默认为1）
13-236		归一化多项式系数，

下一部分：

• 共轭(Conjugate)