Radial NURBS
The acronym NURBS stands for Non-Uniform Rational B-Spline. NURBS are a very general class of curves and surfaces. For a complete discussion of NURBS, which is well beyond the scope of this discussion, see The NURBS Book, Second Edition, by Les Piegl and Wayne Tiller, Springer-Verlag, ISBN 3-540-61545-8.
The radial NURBS surface is defined by a series of weighted control points. The control points define a curve which starts at the origin and lies in the YZ plane along the +Y direction. Once this curve is defined, a figure of revolution is formed by rotating the curve a full 360 degrees around the Z axis. Unlike a spline surface, a NURBS curve does not actually go through the control points, except for the first and last control points. This can be seen in the example below.
'Each control point has a positive "y" coordinate, a "z" coordinate (which may be positive or negative), and a weight "w". The first point is always at y = 0 and z = 0 (as this point cannot be modified by the user, it is defined as control point 0), so the curve begins at the vertex origin of the surface. Subsequent points, numbered from 1 to the maximum number of points desired, extend monotonically outward in the +Y direction. The y values must be spaced at least 1.0E-3 lens units apart for numerical stability in the spline fit. When using this surface to design an imaging system (i.e. one in which wavefront error is an important metric), the z coordinate for control point 1 should be set to zero and the y coordinate for control point 1 should be set to a small fraction of the y coordinate for control point 2 (in this case control point 2 is really the first point of interest on the curve); doing this will avoid discontinuities in the surface shape near the origin which can otherwise lead to erroneous results for the wavefront error.'
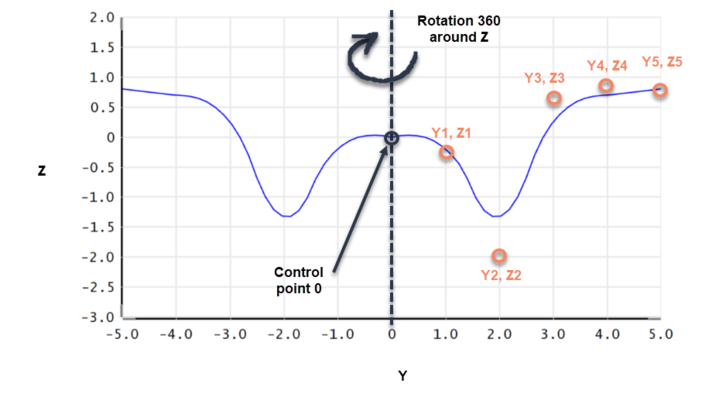
The weights should all be set to 1.0 initially. The higher the weight, the closer the curve will be to the actual control point. Lower weights mean the curve is less constrained to be near the control point. See the above reference for details on the influence of weights on a NURBS curve.
The y value of the last point defined determines the maximum radial clear aperture of the surface. This value should generally be fixed, and not be a variable. Any rays which do not intercept the surface within the defined areas of the curve will be terminated with a "ray miss" error.
The advantage to the NURBS description is that any shape may be defined and traced reliably. Unusual aspheric correctors which cannot be described by polynomials may be modeled as NURBS.
The disadvantages to the NURBS description include very slow ray tracing, and sometimes great difficulty in finding suitable starting values for the control curve points and weights.
This surface does not use any of the parameter columns.
PARAMETER DEFINITIONS FOR RADIAL NURBS SURFACES
| Parameter # | Definition |
| 13 | Number of control points. At least 4 points are required, and no more than 60 allowed. |
| 14 | y coordinate for control point 1. |
| 15 | z coordinate (sag) for control point 1. |
| 16 | w (weight) value for control point 1. |
| 3n+11 | y coordinate for control point n |
| 3n+12 | z coordinate (sag) for control point n |
| 3n+13 | w (weight) value for control point n |
Next:


