Toroidal
Toroidal surfaces are formed by defining a curve in the Y-Z plane, and then rotating this curve about an axis parallel to the Y axis and intersecting the Z axis. Toroids are defined using a base radius of curvature in the Y-Z plane, as well as a conic constant and polynomial aspheric coefficients. The curve in the Y-Z plane is defined by:
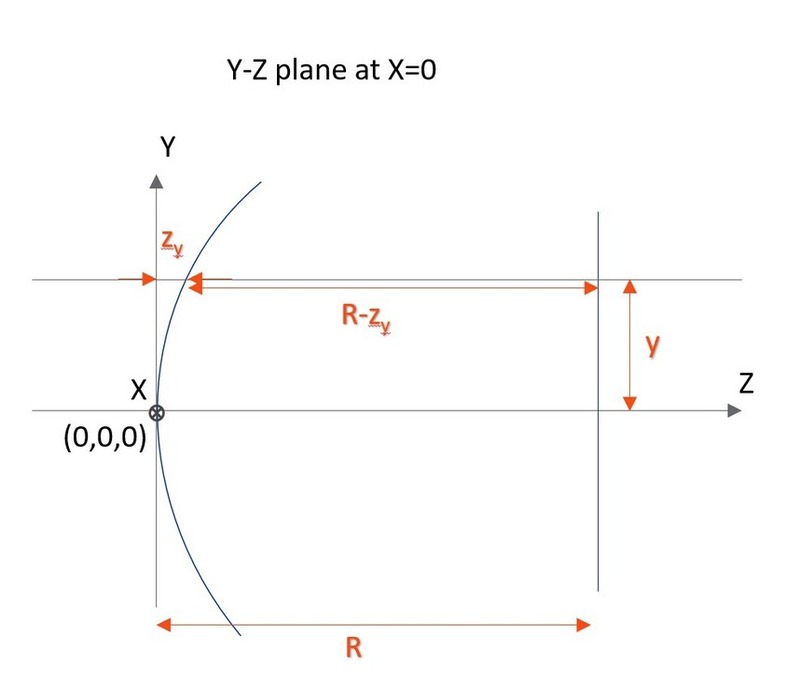
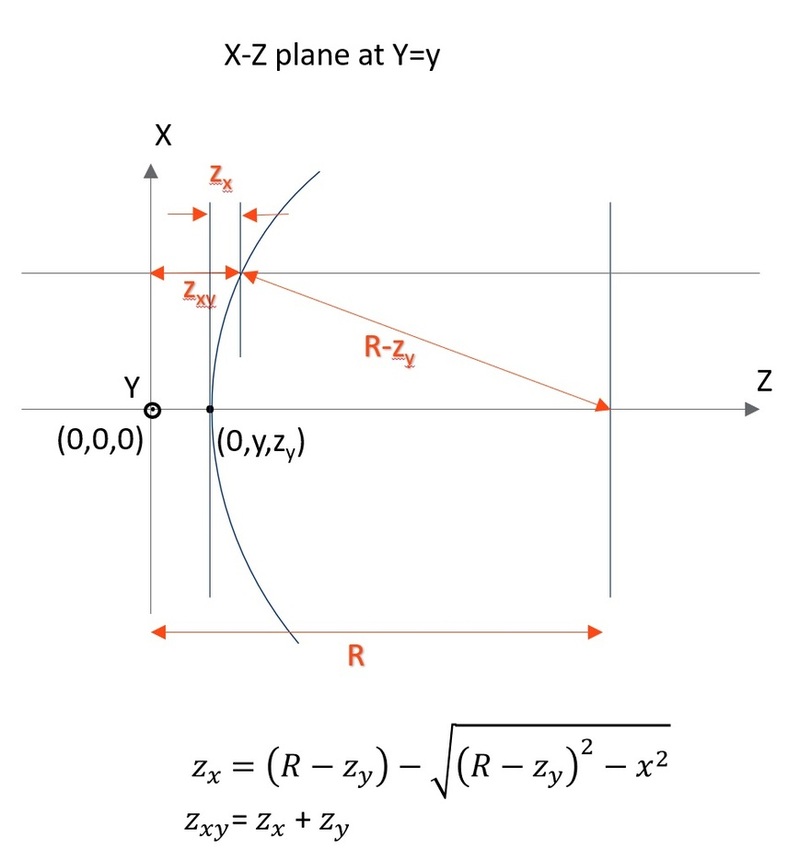
This curve is similar to the even aspheric surface sag formula, except the sixteenth order term has been omitted, and the coordinate argument is y, not r. This curve is then rotated about an axis a distance R from the vertex. This distance R is referred to as the radius of rotation, and may be positive or negative. The Y-Z radius of curvature is specified in the same column on the spreadsheet editor as the radius for Standard surfaces. The radius of rotation is set on parameter column number 1. To model a cylinder lens which is flat in the X direction use zero, which OpticStudio interprets as infinite radius.
The surface may optionally be modified by the addition of the Zernike Standard sag terms:
Where zt is the base toroidal sag and the Zernike Standard terms are defined in the section " Zernike Standard Sag ", and are entered using the Import section of the Lens Data Editor. Note if the Y-Z radius is set to infinity, a surface with power in x but not in y can be described, therefore, the cylinder may be oriented in either direction. The other parameter columns are used for the optional aspheric coefficients, as specified in the following table. If aspheric coefficients are required in the X direction, then rotate the toroid with a pair of coordinate break surfaces and rotate about Z. If different aspheric surfaces are required in both the X and Y directions, see the "biconic", "polynomial" and "extended polynomial" surfaces described elsewhere in this file.
PARAMETER DEFINITIONS FOR TOROIDAL SURFACES
| Parameter # | Definition |
| 0 | Extrapolate |
| 1 | Radius of Rotation, in lens units. |
| 2-8 | α1 - α7 |
| 13 | Number of terms. |
| 14 | Normalization radius. Coordinates are normalized by this value. |
| 15-245 | Coefficients on Zernike polynomials 1 - 231, respectively, in lens units. |
The "Number of terms" is used to specify the maximum Zernike polynomial term to be used in calculating the surface sag. This number is provided to speed the ray tracing calculation; terms beyond this number are ignored.
Zernike polynomials are orthogonal over the unit circle, and so the normalization radius should be set to the radius over which the coefficient data was normalized. Zernike polynomials tend to diverge quite rapidly beyond the normalization radius, and so care should be taken that rays do not strike the surface beyond this radius. Although the ray tracing algorithm may work, the data may be inaccurate. The extrapolate flag may be set to zero to ignore the Zernike terms for rays that land outside the normalization radius.
Next:


