Standard
The most commonly used optical surface is a spherical surface. The sphere is centered on the current optical axis, with the vertex located at the current axis position. OpticStudio treats planes as a special case of the sphere (a sphere with infinite radius of curvature) and conics as a special case as well. The "sag" or z-coordinate of the Standard surface is given by
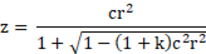
where c is the curvature (the reciprocal of the radius), r is the radial coordinate in lens units and k is the conic constant. The conic constant is less than -1 for hyperbolas, -1 for parabolas, between -1 and 0 for ellipses, 0 for spheres, and greater than 0 for oblate ellipsoids.
For more information on conic constants, see "References on Lens Design".
The Standard surface does not use any of the parameter values.
Modeling an ellipse with the Standard surface
There are a few handy formulas for converting the semi major and semi minor axis lengths of an elliptical surface to a radius and conic description. If "a" is the semi major axis length, and "b" is the semi minor axis length, then
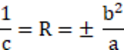
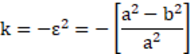
See " Biconic " for an ellipsoid surface that has different semi-axial-lengths in x and y.
Modeling an axicon with the Standard surface
The Standard surface can be used to make an almost perfect axicon. If (1 + k) c 2 r 2 >> 1 , the Standard surface reduces to
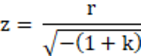
or z = r tan(α), where
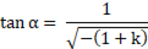
and α is the axicon angle, measured from the XY plane to the axicon surface. To create an axicon, calculate the conic constant value (k) from the angle ( ) desired, and use any small value for the radius of curvature. The resulting value of k must be negative. The exact value of the radius or curvature is not important, as long as it is roughly three or more orders of magnitude smaller than the radial aperture of the axicon. The axicon is not perfect in the sense that there is no cusp at the origin; the region around the surface vertex will be rounded off over a size given approximately by the radius value. This is actually a desirable property for ray tracing, as the surface is everywhere smooth. However, paraxial data, such as effective focal length, magnification, and other common first-order optical properties are not generally meaningful for axicon surfaces. Even though the surface shape is still a conic asphere, the shape of the axicon implies the paraxial properties of the system are not representative of the optical surface as a whole. This is the case for any optical surface that is not well described by the radius of curvature alone.
Next:


