Huygens MTF

Computes the diffraction modulation transfer function (MTF) data using a Huygens direct integration algorithm.
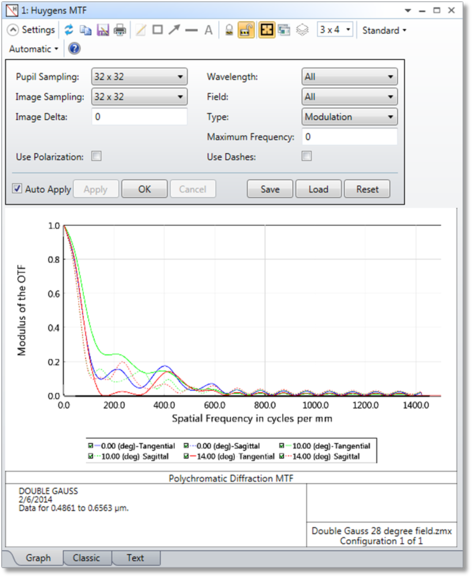
Pupil Sampling Selects the size of the grid of rays to trace to perform the computation. Higher sampling densities yield more accurate results at the expense of longer computation times.
Image Sampling The size of the grid of points on which to compute the diffraction image intensity. This number, combined with the image delta, determine the size of the PSF used to compute the MTF. See also "Huygens PSF" .
Image Delta The distance in micrometers between points in the image grid. Use zero for the default grid spacing.
Configuration Select "All" to perform a calculation of the MTF based upon a coherent sum of the PSF at each wavelength across all configurations, or select the "Current" or any single configuration. Note the MTF is computed from the PSF, which is a coherent sum for the same wavelength in each configuration, followed by an incoherent sum of the resulting PSF's for different wavelengths. For this reason, each defined wavelength must be the same in all configurations. Wavelength and configuration weights may be used but the wavelength values must be identical. See CWGT and WLWT in "Summary of multi- configuration operands. This coherent sum also assumes that the image surface is located in the identical position in all configurations. If "All" is selected, and both focal and afocal mode configurations are defined, the Configuration setting will automatically be reset to "Current".
Wavelength The wavelength number to be used in the calculation.
Field The field number for which the calculation should be performed.
Type Select the data to display, currently modulation is the only option.
Max Frequency The maximum frequency in MTF units (see "MTF Units") to display.
Use Polarization If checked, polarization is considered. See "Polarization (system explorer)" for information on defining the polarization state and how polarization is used by analysis features.
Use Dashes Selects either solid lines or dashed lines to differentiate the various curves. This setting only applies to the Classic view, which is an option if "Enable Classic View" is selected in the Graphics tab of the OpticStudio Preferences.
Discussion
See the discussion sections of the Huygens PSF. Those comments also apply to this feature.
The Huygens MTF computes an FFT of the Huygens PSF. The settings for Image Sampling and Image Delta are the same as for the Huygens PSF, therefore it is instructive to do a Huygens PSF first (see "Huygens PSF"). Since the transform is done on the PSF in image space coordinates, the tangential response corresponds to spatial frequencies in the y direction in local image surface coordinates, and the sagittal response corresponds to spatial frequencies in the x direction. The Huygens MTF also has no dependence on the location of rays in the paraxial pupils. The MTF can therefore be computed for any system that the Huygens PSF can be computed for including many non-sequential systems using ports where reference rays required by other diffraction algorithms would not make it through, or for systems where pupils or images formed by multiple non- sequential sub-apertures are overlapped. Systems with extreme exit pupil distortion, such as very fast off-axis reflectors, are also handled correctly with the Huygens technique.
The nature of the Huygens algorithm is that the computation is done in image space coordinates. For this reason, rotating the image surface will affect the orientation of the computed MTF. The tangential response corresponds to the image of a periodic target oriented with lines along the image space X axis, and the sagittal response corresponds to the image of a periodic target oriented with lines along the image space Y axis. This is different from the conventions of the "FFT MTF"
Next:


