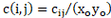Chebyshev Polynomial

The Chebyshev Polynomial surface is a freeform surface that is described by a base radius of curvature and a sequence of Chebyshev polynomials. A one-dimensional Chebyshev polynomial of the first kind is given by:

For reference, the first ten Chebyshev polynomial coefficients are the following:

T₀ (x) = 1

T₁ (x) = x

T₂ (x) = 2x² – 1

T₃ (x) = 4x³ - 3x

T₄ (x) = 8x⁴ - 8x² + 1

T₅ (x) = 16x⁵- 20x³ + 5x

T₆ (x) = 32x⁶ - 48x⁴ + 18x² – 1

T₇ (x) = 64x⁷ - 112x⁵ + 56x³ - 7x

T₈ (x) = 128x⁸ - 256x⁶ + 160x⁴ - 32x² + 1

T₉ (x) = 256x⁹ - 576x⁷ + 432x⁵ - 120x³ + 9x

T₁₀ (x) = 512x¹⁰ - 1280x⁸ + 1120x⁶ - 400x⁴ + 50x² - 1

The transition to a two-dimensional Chebyshev polynomial is done using the product basis t_ij (x,y) :

In OpticStudio, the maximum order for both x and y is set to 14. Any function may be interpolated as a finite sum of Chebyshev polynomial terms:

The arguments of the 2D Chebyshev polynomials are defined on the unit interval. To make the interpolation valid for an arbitrary interval, we use normalized and as the arguments of the polynomials.

Then the "sag" or z-coordinate of the Chebyshev polynomial surface is given by:

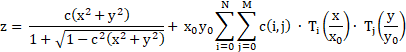
where c is the curvature at the vertex of the surface, and are the normalization lengths, and are the normalized polynomial coefficients .

Chebyshev surfaces are not defined outside of the normalization radii, X0 and Y0. Rays that strike a Chebyshev surface outside of the normalization radii cannot be traced and will be vignetted at the Chebyshev surface.

PARAMETER DEFINITIONS FOR CHEBYSHEV POLYNOMIAL SURFACES


Parameter #	Name	Definition
1	Max X Order	Maximum Polynomial Order in X-coordinate (integer, up to 14)
2	Max Y Order	Maximum Polynomial Order in Y-coordinate (integer, up to 14)
3	Norm X Length	Normalization length (positive, 1.0 by default)
4	Norm Y Length	Normalization length (positive, 1.0 by default)
13-236		Normalized polynomial coefficients,

Next:

Conjugate