Perturbation Method for Passivity Enforcement

The passivity by perturbation method is selected with (s_element.passivity_enforcement=6). With this method, passivity enforcement of scattering parameter data with larger numbers of ports is achieved by the perturbation of the singular values of the transfer function matrix.

The frequency-domain transfer function matrix H (jw):

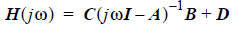
is obtained on the transfer matrix fit to the S-parameter data S(jw).

The singular values of the transfer matrix s[H (jw)] are the square roots of the eigenvalues of [H ^H(jw)H (jw)], where H ^H(jw) denotes the complex conjugate transpose of H (jw).

For passivity, the singular values of the transfer matrix must be less than or equal to 1 for all frequencies.

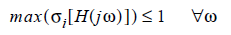
The perturbation method is derived on the eigenvalue (modal) perturbation of [H ^H(jw)H (jw)], equivalent to the perturbation of the singular values of H (jw). Higher order terms are ignored. As a first step, the D matrix is passified to guarantee asymptotic passivity. Next, linear perturbation is applied iteratively to the C matrix, minimizing the norm of the perturbation and the transfer matrix deviation at each iteration.

Generally, a nonpassive singular value exceeds the threshold only over a range of frequencies. The method uses the slope of the curve at the points where the singular value crosses the threshold to determine the direction of the perturbation to be applied.

The perturbation method generates matrices of approximate size k * N* (P+Q), where N is the number of states and k is the number of singular values that are greater than 1. Thus, this method is applicable to systems with large numbers of ports.