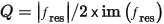Resonant Frequencies

Almost any PCB and chip package that contains power/ground plane structures has resonances at certain frequencies. Whether a resonance is excited depends on the location of a source and the frequency content of its signal.

The best way to view the natural resonances, and to what extent electromagnetic energy sources excite them, is to model the entire structure.

To model the structure:

1. Calculate the natural resonances/Eigen modes.

   Natural resonances are points at which the resonant frequencies are a function of the position of the PCB(s) and other components, and how/where the PCB ground plane bonds to the enclosure.

   SIwave employs a 2D Eigen solver to establish the natural resonant frequencies in the power-ground structure and the field distributions or Eigenmodes associated with them. The natural resonances are the resonances that may occur in the power/ground structure if there is an electromagnetic source that excites them. However, since the Eigen solver computes natural cavity resonances, no actual sources are involved.

2. Apply excitations.

   Modeling the application of one or more excitations establishes how they couple into the natural resonances. Excitations, over a range of frequencies, are applied at ports. At certain frequencies, typically the ones identified as Eigen frequencies earlier, little energy will be reflected back into the exciting port. The energy is trapped in an Eigen mode. Eventually, part of it will be dissipated in losses in the structure, and part of it will be accepted by ports. The fact that there is a dip in the return loss of a certain port at a certain frequency serves as a warning that an electromagnetic source at this location may excite a natural resonance at this frequency, usually leading to inappropriate behavior of the device. Based on this information, you can make changes, such as the insertion of decoupling capacitors, and then analyze the altered device.

   The resonant frequency analysis is typically followed by a frequency sweep of voltages and currents.

In Resonant Mode Analysis

The real part of the resonance frequency ƒ_res is the frequency at which the mode oscillates. The imaginary part of the resonance frequency determines the rate at which the mode decays. The behavior of the mode vs. time in the absence of any excitation is calculated using:

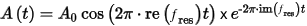
Where A₀ is the initial amplitude at time t = 0, im() is the imaginary part, and k is the free space wave number, calculated as:

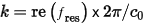
Where c₀ is the speed of light in a vacuum and re() is the real part.

The free space wavelength is calculated as:

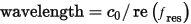
Q is the quality factor, calculated as: