Passivity Checking: Convex Programming Method
By the Bounded Real Lemma, the state-space system ABCD is passive if a positive definite matrix K>0 exists such that:
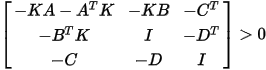
The convex programming method preserves the poles from the original state formulation (state matrix A). The formulation is such that the estimate of matrix B is not needed. For a fixed matrix A, the method recomputes matrices C and D to minimize errors while observing the Bounded Real Lemma.
The convex method of passivity enforcement is guaranteed to produce a passive state-space realization, but is very slow and memory-intensive. Convex optimization requires computing the Hessian or second derivative matrix, with dimension (P+Q)2 by (P+Q)2, where P+Q is the total number of input and output ports. The total memory requirement for the matrices is (P+Q)4. The compute time to solve the matrices is (P+Q)6. In practice, the exponential growth of the solution size limits the convex programming method to systems with the total number of ports (P+Q) less than or equal to 10.
