Viewing Convergence Data for 2D Extractor
2D Extractor performs adaptive analysis for accurate simulations. It uses “h-adaptive” mesh refinement, iteratively refining the initial mesh by reducing the size of individual elements in areas of high approximation error—thus improving the accuracy of the solution. Different convergence control mechanisms such as Energy Error, Loss Error and Parameter Error exist are used during the analysis.
To view convergence data:
- From the Project Manager, right-click a solution setup and select Convergence.
The Solutions dialog box appears, with the Convergence tab selected.
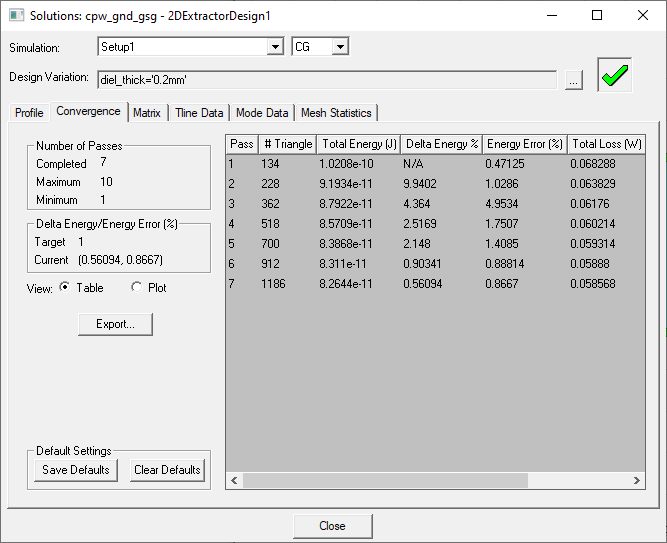
Convergence Data includes:
- Number of Adaptive Passes – during the solution process, this information includes the number of solve → error analysis → refine cycles completed / yet to be completed. After analysis has completed, only completed cycles are listed.
- Number of Triangles – the number of tetrahedra or triangles created at each adaptive pass. For magnetic materials, convergence data shows information for surface mesh triangles.
- Total Energy – the energy stored in the electric and magnetic fields over the entire computational domain, in Joules.
- Delta Energy – the percentage change in the total energy from the previous adaptive pass k-1 to the current pass k, expressed as a percentage of the energy in the current pass.
- Energy Error – a metric for estimating the error in the finite element solution.
- Total Loss – power loss measured over the entire computational domain.
- Delta Loss – the percentage change in the total loss from one pass to the next.
- Loss Error – the error in the losses computed by the finite element solution.
- See Convergence Criteria below for additional details.
Use the radio buttons to switch between Table view (shown above) and Plot view:

Convergence Criteria in 2D Extractor
| Parameters | Description |
| Total Energy | Total Energy is the energy stored in the electric and magnetic fields over the entire computational domain, in Joules. For CG solutions, Total Energy can be written as:
Where:
For RL solutions, Total Energy can be written as:
Where:
The capacitance (C) and inductance (L) values are closely related to the Total Energy. For CG or RL matrices, these values can be derived from the Total Energy stored in the system under certain excitation configuration (for example, an excitation configuration of 1A for one signal line and 0A for all others is used in eddy current solution, which results in L to be directly proportional to the total magnetic energy as L=2*Total Energy). A good indication of accurate C and L values is when the total energy stabilizes during the adaptive refinement process. |
| Delta Energy | Delta Energy is the percentage change in the Total Energy (as defined above) from the previous adaptive pass k-1 to the current pass k, expressed as a percentage of the energy in the current pass:
Delta Energy is calculated for |
| Energy Error | A finite element solution approximates the electric and magnetic fields in the problem domain using low-order polynomial basis functions. Energy Error is a metric for estimating the error in the finite element solution. It should decrease as the mesh is refined. Energy Error is displayed as a percentage of the Total Energy. In a well-converged solution, the Energy Error should be much less than the Total Energy. By default, Delta Energy and Energy Error are used for convergence of the solution during the adaptive process, unless you select one of the CG/RL Advanced options: Use Loss Convergence or Use Parameter Convergence. |
| Total Loss | Total loss is the power loss due to mechanisms such as Joule I-R heating (Ohmic loss), dielectric dissipation (loss in dielectric materials with loss tangent under alternating electric fields) and non-ideal magnetic materials (Hysteresis loss in magnetic materials under alternating magnetic fields), measured over the entire computational domain. The total loss is displayed for AC conduction or Eddy Current solutions, in Watts. The conductance (G) and resistance (R) values are closely related to the Total Loss. For CG or RL matrices, the values can be derived from the Total Loss in the system under certain excitation configuration (for instance, an excitation configuration of 1A for one signal line and 0A for all others is used in Eddy Current solution, which results in R to be directly proportional to the Total Loss as:
When Total Loss stabilizes during adaptive refinement , this is a good indicator that the G and R values will be accurate. |
| Delta Loss | Delta loss is analogous to delta energy. It is the percentage change in the total loss from one pass to the next one as formulated below:
Delta Loss is calculated for |
| Loss Error | Loss Error is a metric used to estimate the error in the losses computed by the finite element solution. It should decrease as the mesh is refined. Loss Error is displayed as a percentage of the total loss. In a well converged solution, the Loss Error should be much less than the Total Loss. Delta Loss and Loss Error criteria are used during the adaptive process only if the CG/RL Advanced option Use Loss Convergence is selected. |

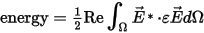
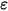 is the effective complex permittivity
is the effective complex permittivity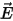 is the electric field vector
is the electric field vector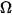 denotes the problem domain
denotes the problem domain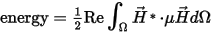
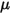 is the effective complex permeability
is the effective complex permeability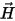 is the magnetic field vector
is the magnetic field vector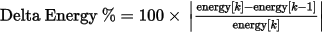
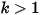 .
.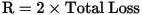
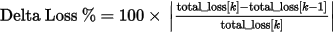
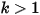 , where k is the current adaptive pass number.
, where k is the current adaptive pass number.