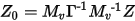Modal Analysis of Lossy Transmission Lines

A system of N lossy, coupled transmission lines is defined by its length l and by its set of per-unit-length circuit parameter matrices R,L,G, and C. These matrices are N x N and are typically frequency dependent. It is convenient to also define per-unit-length impedance Z(jω) and admittance matrices Y(jω) as follows:

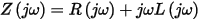
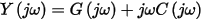
The frequency-domain telegrapher equations for the transmission lines are then defined as:

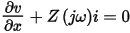
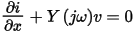
Here v and i are N x 1 vectors representing respectively the voltages and currents on the transmission lines. Both are functions of the frequency ω and the position variable x, which ranges from 0 to l.

The telegrapher equations can be combined into a second-order differential equation by differentiating the first equation with respect to the position variable x and then using the second to eliminate the derivative of the current:

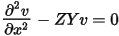
This is a set of coupled differential equations. To make it possible to solve them, we can decouple the equations using the eigenvectors of the matrix ZY.

Let the eigenvector decomposition be:

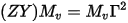
where M_v is a matrix whose columns represent the eigenvectors (voltage modes) and

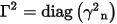
is a diagonal matrix whose entries γ²_n are the eigenvalues of ZY.

Define a vector of modal voltages 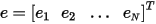related to the total voltages v by the transformation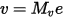

Using this definition we can transform the coupled second-order differential equations into a system of uncoupled equations:

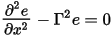
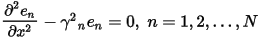
These equations have simple analytic solutions:

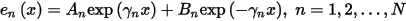
Here the coefficients A_n and B_n are determined by the voltages at the ends of the transmission line. The first term corresponds to a backward-traveling modal wave, and the second corresponds to a forward-traveling wave.

The propagation constants γ_n are complex numbers with real part α_n and imaginary part β_n.

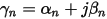
It can be seen that α_n represents the attenuation per unit length that the mode experiences as it moves down the transmission line. The imaginary part β_n represents the change in phase per unit length.

A change in phase of 2π constitutes one wavelength; therefore the effective wavelength λ_n of mode n satisfies β_nα_n = 2π

So:

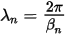
The phase velocity c_n of the n-th mode satisfies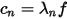

So the velocity is:

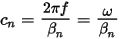
ε_n

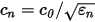
Therefore we can define an effective permittivity for the n-th mode:

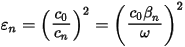
Finally we note that it is possible to define a characteristic impedance matrix Z₀for the system of transmission lines. This is a matrix that describes the ideal, reflection-free termination for the system of transmission lines. It is possible to express it as: